2014-02-02
430
На основе ФНЧ синтезированного рассмотрено способом с помощью приема, называемым преобразованием частоты, могут быть получены передаточные функции и схемы ФВЧ и полосовых фильтров. Заменим передаточной функцией ФНЧ переменную Р новой переменной Р’ такой, что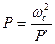 
(*)
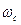— частота среза.
Рассмотрим теперь каким образом при этом трансформируются основные характерные точки характеристики ФНЧ.
Точке Р = 0 соответствует бесконечно удаленная точка b’ плоскости P’. Точкам резкого изменения частотной характеристики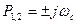 
будут соответствовать 
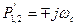, отличающиеся от исходных лишь измененным знаком. Бесконечно удаленные точки 
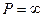будут соответствовать P’ = 0.
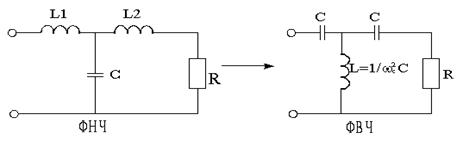
Т.о. можно ожидать, что АЧХ фильтра синтезированного с помощью преобразования (*) будут соответствовать ФВЧ, при этом каждый конденсатор, имевший в схеме ФНЧ проводимость РС должен быть изменен на элемент с проводимостью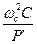 
, т.е. на катушку индуктивности 
. Аналогично катушка с индуктивностью L в ФНЧ должна быть заменена на конденсатор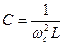 
. Резисторы в этой схеме остаются без изменения. Этот переход показан на рисунке.
|
|
|
Полосовой фильтр с малым ослаблением пропускает лишь частоты в полосе, примыкающей к некоторой частоте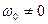 
. Если синтезировать ФНЧ с заданной 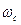, то можно получить передаточную функцию схемы ПФ, сделав замену 
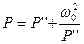. При этом точки 
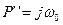соответствуют P = 0. Т.о. максимальная АЧХ, наблюдавшаяся в ФНЧ на нулевой частоте возникает в ПФ на частоте 
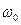, т.к. 
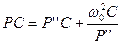проводимости конденсатора, примененного в схеме ФНЧ, соответствующая схеме ПФ проводимость параллельного контура, образованного конденсатором C и катушкой индуктивности 
.
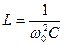Аналогично из равенства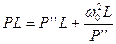 
заключаем, что катушка L превращается в последовательное соединение катушки L и конденсатора 
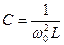, т.е. последовательный колебательный контур. Этот переход показан на рисунке.
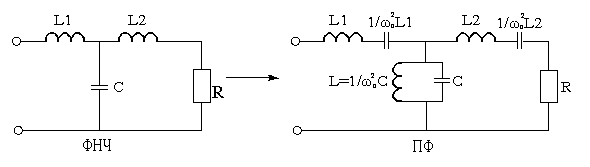
Т.о. при синтезе фильтров ФНЧ служит фильтром прототипом, параметры которого дают возможность перейти к схемам других фильтров. При этом точность аппроксимации желаемых характеристик нового фильтра эквивалентна точности аппроксимации ФНЧ.
