Ломаные Эйлера

Доказательство теоремы существования решения задачи Коши основано на построении ломаных Эйлера и лемме о хорде ломаной.

Рассмотрим ломаную линию 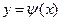, состоящую из 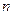звеньев. Обозначим через 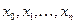- абсциссы угловых точек ломаной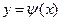, а через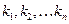– угловые коэффициенты её звеньев.

Лемма. Если угловые коэффициенты звеньев ломаной 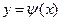заключены между числам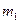и и ,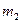

,

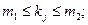
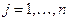то угловой коэффициент 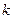всякой хорды этой ломаной также заключён между этими числами

Доказательство. Пусть концы произвольной хорды с угловым коэффициентом 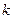имеют абсциссы 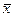и 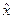. Тогда справедливо равенство

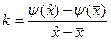
Отрезки 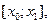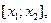…, 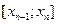– проекции звеньев ломаной 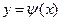на ось 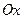, поэтому для каждого углового коэффициента звена ломаной будет иметь место равенство

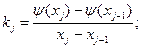
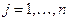
Обозначим через 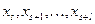те абсциссы вершин ломаной 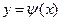, которые находятся между точкам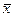и и 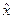. Тогда можно записать следующую систему равенств

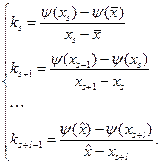
Перепишем полученную систему соотношений следующим образом

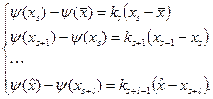
Сложим полученные равенства, тогда, сокращая слева все полученные слагаемые, кроме двух, будем иметь

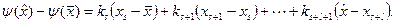
Величины 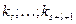– угловые коэффициенты звеньев ломаной, поэтому они удовлетворяют неравенствам 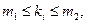где 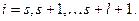Таким образом, разность 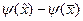можно ограничить сверху и снизу. Чтобы получить оценку снизу, все величины 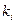заменим на величину 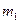. Для получения оценки сверху заменим 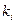на величину 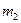. Получится

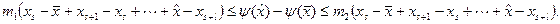
В скобках справа и слева также сокращаются почленно все слагаемые, кроме двух. Тогда

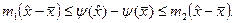
Отсюда

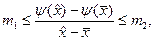
что и доказывает лемму.

Утверждение леммы справедливо для ломаной линии, состоящей из любого конечного числа звеньев.

Пусть теперь дано дифференциальное уравнение

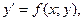(1)

где переменные и изменяются на некотором множестве 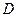на плоскости 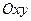. Выберем на множестве 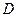произвольную точку 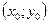и добавим к уравнению (1) начальное условие

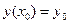. (2)

Предположим, что для уравнения (1) на множестве 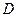выполняется теорема существования решения задачи Коши (1)-(2). Через точку 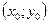проведём прямую с угловым коэффициентом, равным 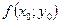. На этой прямой отметим другую точку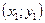, так чтобы 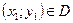. Через эту точку проведём новую прямую с угловым коэффициентом, равным 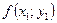и на этой прямой отметим точку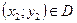. Будем продолжать этот процесс, пока не дойдём до границы множества 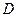. У нас получится набор точек 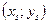. Проходящая через них ломаная линия называется ломаной Эйлера.

Величины будут вычисляться по формулам

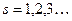
Из этого представления следует, что

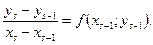
Исходя из вида последнего равенства, можно предположить, что если брать точк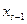и и 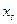достаточно близко друг к другу, то построенная ломаная должна давать некоторое приближённое представление о поведении интегральной кривой уравнения (1). Можно также предположить, что при неограниченном уменьшении расстояния между точкам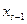и и 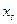ломаная Эйлера будет неограниченно приближаться к интегральной кривой уравнения (1), проходящей через точку 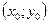. При доказательстве теоремы Пеано мы действительно установим, что если функция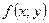непрерывна на множестве 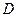по переменным 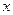и 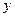, то можно построить последовательность ломаных Эйлера, которая будет сходиться к интегральной кривой уравнения (1), проходящей через точку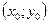. Однако, такая кривая, вообще говоря, не будет единственным решением задачи Коши, т.е. через указанную точку могут проходить и другие интегральные кривые того же уравнения. Для того, чтобы через точку 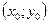проходила одна и только одна интегральная кривая уравнения (1), нужно дополнительное условие на функцию 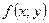, которое в теореме Пикара называется условием Липшица.