Локальная предельная теорема

Задача прибл. вычисления 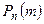и 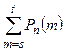была решена А. де Муавром.

Локальная теорема Муавра. Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна p (0< p <1), то вероятность 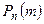того, что в этих испытаниях событие А наступит ровно m раз, удовлетворяет при 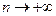соотношению 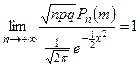равномерно для всех m, для которых 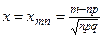находится в каком-нибудь конечном интервале. Д-во. [5, с. 78-80].

Замечание. Тогда 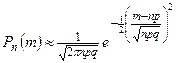(можно приближённо вычислить).

Аналогичную теорему можно сформулировать и доказать для полиномиального распределения.

Пример. Пример 2 предыдущего параграфа, 0,00206 (точные подсчёты 0,00197).