Интегральная предельная теорема

Интегральная теорема Муавра-Лапласа. Если µ есть число наступлений события в n независимых испытаниях, в каждом из которых вероятность этого события равна р, причём 0< p <1, то равномерно относительно а и b (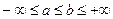)имеет место соотношение 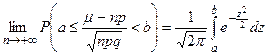. Д-во. См. [5, с. 85-89].

Замечание. Интегральная теорема Муавра-Лапласа является частным случаем интегральной предельной теоремы.

Пусть 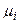(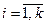) означает число появлений событий 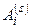(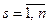) в n последовательных испытаниях. В зависимости от случая 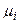могут принимать лишь значения 0, 1, 2, 3, …, n, причём так как в каждом испытании возможны k исходов и эти исходы несовместимы, то должно иметь место равенство: 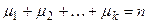. (1)

Будем рассматривать величины 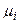(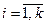) как прямоугольные координаты точки в k -мерном евклидовом пространстве.

При этом результаты испытаний изобразятся точкой с целочисленными координатами, не меньшими нуля, не большими n; в дальнейшем будем называть такие точки целочисленными. Равенство (1) показывает, что результаты испытаний изобразятся не произвольными целочисленными точками в гиперкубе (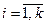), а лишь теми из них, которые находятся в гиперплоскости (1).

Произведём преобразование координат по формулам 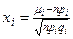(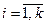, 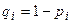). Уравнение гиперплоскости (1) в новых координатах перепишется в следующем виде 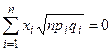. (2)

Точки гиперплоскости (2), в которые перешли целочисленные точки гиперплоскости (1), будем также называть целочисленными.

Обозначим 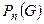вероятность того, что в результате n испытаний числа 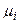(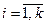) появления каждого из возможных исходов окажутся такими, что точка с координатами 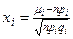попадёт внутрь области G. Тогда имеет место следующая теорема:

Теорема. Если в схеме последовательных независимых испытаний в каждом из испытаний возможны k исходов, причём вероятность каждого из исходов не зависит от номера испытания и отлична о 0 и от 1, то какова бы ни была область G гиперплоскости (2), для которой (k-1) – мерный объём её границы равен нулю, равномерно относительно G имеет место соотношени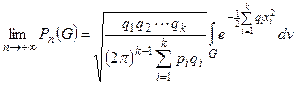е , где 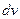означает элемент объёма области 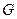, интеграл вычисляется по области G.