Задачи, приводящие к теорем Муавра-Лапласа. Приложения интегральной теоремы Муавра-Лапласа

Приложения интегральной теоремы Муавра-Лапласа

1. Закон больших чисел (неравенство Бернулли). .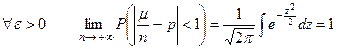

Неравенство Бернулли позволяет использовать построения теории вероятностей при решении многих задач естествознания и техники.

Проводится n независимых испытаний, при каждом из которых вероятность наступления события P(А)= р.

1. Чему равна вероятность того, что частота наступления события А отклонится от вероятности р не более чем на α?

.

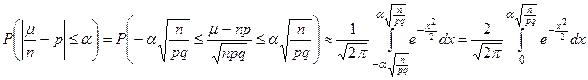2. Какое наименьшее число испытаний нужно произвести для того, чтобы с вероятностью, не меньшей β, частота отклонялась от вероятности не больше чем на α?

Нужно определить n из неравенства 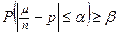. Вероятность, стоящую в левой части неравенства, приближённо заменим по теореме Муавра-Лапласа интегралом. В результате для определения n получится неравенство .

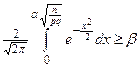3. При данной вероятности β и числе испытаний n требуется определить границу возможных изменений 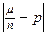. Другими словами, зная β и n, нужно найти α, для которого 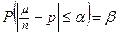. Применение интегральной теоремы Лапласа даёт для определения α уравнение .

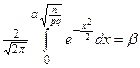Определение. Функция 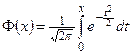называется функцией Лапласа.

Замечание. Так как 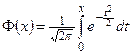в конечном виде через элементарные функции не выражается, то для вычисления 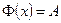, а также для решения обратной задачи – вычисления х по заданному А, используют специальные таблицы и свойства функции Лапласа.

1. Нечётность.

2. Непрерывность.

3. .

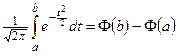4. График.

Пример 2. Вероятность изделию некоторого производства оказаться бракованным равна 0б005. Чему равна вероятность того, что из 10000 наудачу взятых изделий бракованных изделий окажется не более 70?

Решение. n=10000, p=0,005. Поэтому по формуле (1) находим вероятность того, что число бракованных изделий окажется не больше 70, равна сумме вероятностей числу бракованных изделий оказаться равным 1, 2, 3, …, 70. Таким образом: .

По интегральной теореме Муавра-Лапласа

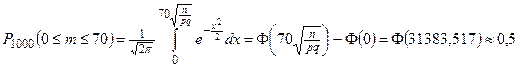
Замечание 1. Значения (…) в таблице значений функции Лапласа нет. Все значения, большие 5, заменяются значением при х =5, погрешность при этом составляет менее .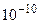

Замечание 2. Если значения р и q не слишком близки к 0 и 1, то интегральная теорема Муавра Лапласа даёт удовлетворительные результаты, но при р и q близких к 0 или 1это представление работает плохо. Для того, чтобы в этом случае теорема Муавра-Лапласа дала хороший результат, требуется, чтобы n было очень велико.