Теорема Пуассона. Пуассон доказал асимптотическую формулу, приспособленную для малых р

Пуассон доказал асимптотическую формулу, приспособленную для малых р.

Теорема Пуассона. Если в последовательности серий испытаний события каждой серии взаимно независимы между собой и имеют каждое вероятность 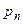, зависящую только от номера серии, а 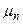- число фактически появившихся событий n -ой серии, тогда из 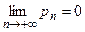следует, что .

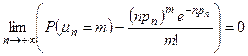Доказательство. См [5, C. 98 – 99].

Обозначим 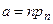, будем предполагать, что эта величина слабо меняется от серии к серии, обозначим .

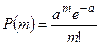Определение. Распределение вероятностей 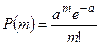называется законом Пуассона.

Замечание. .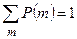

Свойства 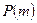как функции m. Рассмотрим отношение .

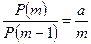Если 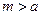, то 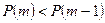, если же 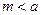, то 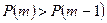. Если 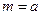, то 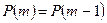. Отсюда следует, что величина 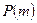возрастает при увеличении m от 0 до 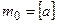и при дальнейшем увеличении m убывает. Если а – целое число, то 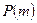имеет 2 максимальных значения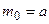: при и при .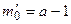

Пример. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.