Погрешности формул численного интегрирования. При численном интегрировании возникают два типа погрешностей: 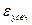и

При численном интегрировании возникают два типа погрешностей: и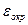

Погрешность усечения возникает из-за замены функции f(x) на интерполирующий ее многочлен. Погрешность округления возникает из-за того, что значение функции y_i в узлах интерполяции известно не точно, а приближенно, с некоторой погрешностью η.

Теорема 5.2:

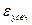(с учётом знака) для формулы трапеции (5.12)

(5.15)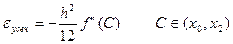

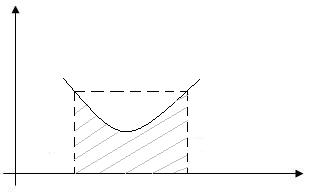Комментарии: если f”>0, то 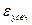<0 ()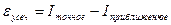

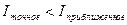
Теорема 5.3:

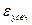(с учётом знака) для формулы Симпсона:

(5.16)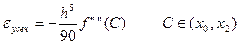

Замечания:

Из (5.15) видно – формула трапеций выдаёт правильный результат (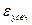=0), если f – многочлен первой степени (т.к. f”(x)=0). Этого следовало ожидать, т.к. при выведении формулы трапеции мы заменяли f(x) на И.М. её первой степени, который совпадает с f(x).

По этой причине логично ожидать, что 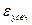для формулы Симпсона будет нулевой, если f – многочлен второй степени (т.к. в формуле Симпсона происходит интерполяция по трём точкам). Как мы видим из (5.16) формула Симпсона будет верна не только для многочлена третей степени, т.к. f””(x)=0.