Погрешности общих формул трапеции и Симпсона

Погрешности усечения общей формулы трапеции и общей формулы Симпсона состоят из суммы погрешностей усечения формулы трапеции и формулы Симпсона на каждом интервале.

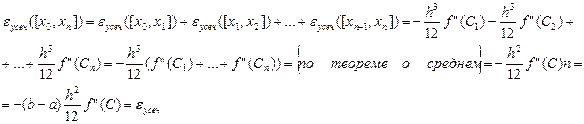
для общей формулы трапеции (5.17):

(hn=b-a) (5.19)

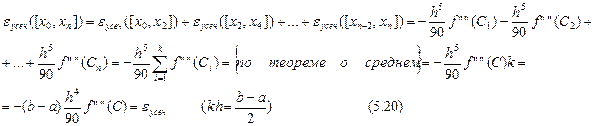Аналогично выводим для общей формулы Симпсона (5.18):

Т.к. местоположение точек С нам не известно, то (5.19) и (5.20) мы заменяем на оценки сверху (2.3 max соответствующих производных).

Для формулы трапеции:

(5.21) 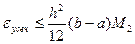, где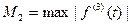

(5.22) 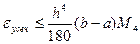, где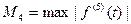

Погрешность округления общей формулы трапеции и общей формулы Симпсона:

Для формулы трапеции:

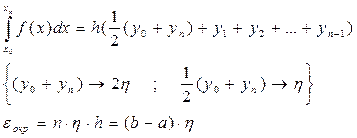
Аналогично для формулы Симпсона:

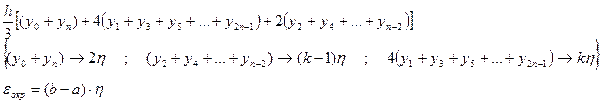
6.6. Метод двойного пересчёта для оценки погрешности численного интегрирования.

При практических вычислениях часто бывает затруднительно оценить погрешность усечения формулы трапеции или формулы Симпсона из-за того, что надо находить max 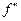или 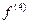. В этом случае используется метод двойного пересчета.

Заметим, что при уменьшении шага в 2 раза, 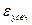в формуле трапеций уменьшается в 4 раза, а в формуле Симпсона в 16 раз.

Поэтому поступим следующим образом: вычислим интеграл на (a,b) дважды – с шагом h и h/2.

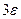
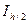
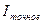
(рис.1)

если I_h - I_h/2 <3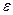, то | I_h/2 – I_точное |<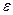. И поэтому в начале точное значение интеграла можно взять I_h/2 (оно будет найдено с заданной точностью).

Итак, при вычислении интеграла с помощью двойного пересчёта поступаем следующим образом: I_h - I_h/2 <3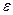, I_точное = I_h/2

если точность не достигнута, то шаг h уменьшаем в 2 раза, находим 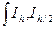и так далее, пока точность не будет достигнута.

Замечание:

Формула трапеции имеет 2-ой порядок точности, т.к. в оценке 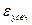для глобальных формул трапеции (имеется в виду глобальный вариант формулы (т.е. применяем формулу на одном и том же интервале)) 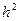и поэтому при уменьшении шага в k раз - 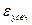уменьшается в 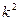раз.

Формула Симпсона имеет 4-ый порядок точности, т.к. .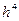

6.7. Метод коррекции в двойном пересчёте.

Как видно из графика (рис.1),при двойном пересчёте в качестве I_{точного} выгодно использовать не I_h/2, а:

I = I_h/2+1/3(I_h/2-I_h) = I_кор

После коррекции по этой формуле точность метода возрастает на порядок, т.е. метод трапеции будет не второго, а третьего; а Симпсона – пятого порядка точности.

При использовании формулы Симпсона в методе двойного пересчета вместо 3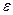будет 15.

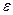Если |I_h-I_h/2 |<15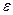, то I_h/2 – значение интеграла с погрешностью, не больше .

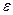Тема 6: Численные методы решения дифференциальных уравнений и систем дифференциальных уравнений (ДУ и СДУ).