2014-02-02
657
Определение 1. Непрерывная случайная величина называется распределённой логарифмически-нормально (логнормально), если её логарифм подчинён нормальному закону распределения.
Так как при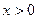 
неравенства 
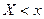и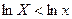 
равносильны, то функция распределения логнормального распределения совпадает с функцией нормального распределения для случайной величины 
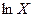, т.е.
, 
.
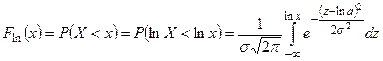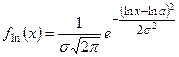Можно доказать, что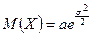 
, 
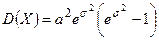, мода 
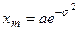, медиана 
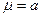. Упражнение: доказать.
Логнормальное распределение используется для описания распределений доходов, банковских вкладов, цен активов и т.д.
