Функции двух случайных аргументов
Определение1. Если каждой паре возможных значений случайных величин Х и У соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов Х и У:  .
.
Задача нахождения распределения функции 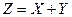 является важной в практическом смысле (теория измерений, определение погрешностей).
является важной в практическом смысле (теория измерений, определение погрешностей).
Правило 1. Пусть Х и У – дискретные независимые случайные величины. Для того, чтобы составить закон распределения функции 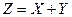 , надо найти все возможные значения Z и их вероятности. Возможные значения Z есть суммы всех возможных значений Х со всеми возможными значениями У, вероятности которых соответственно равны произведениям вероятностей соответствующих значений Х и У. Если у величины Z получилось несколько одинаковых значений, то их вероятности складываются.
, надо найти все возможные значения Z и их вероятности. Возможные значения Z есть суммы всех возможных значений Х со всеми возможными значениями У, вероятности которых соответственно равны произведениям вероятностей соответствующих значений Х и У. Если у величины Z получилось несколько одинаковых значений, то их вероятности складываются.
Пример 1. Пусть случайные величины Х и У заданы своими законами распределения. Найти закон распределения функции 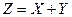 .
.
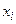 |  | |||||
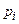 | 0,4 | 0,6 | 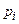 | 0,2 | 0,8 |
 2014-02-02
2014-02-02 2444
2444
