Понятие о центральной предельной теореме Ляпунова

Закон больших чисел устанавливает факт приближения средней арифметической большого числа случайных величин к определённым постоянным. Но при некоторых условиях совокупное действие случайных величин приводит к нормальному закону распределения. Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.

Теорема Ляпунова. Если , , 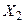…, 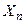–независимые случайные величины, у каждой из которых существует математическое ожидание 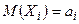, дисперсию 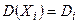, абсолютный центральный момент третьего порядка 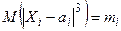и 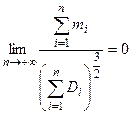, то закон распределения суммы 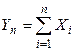при 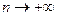неограниченно приближается к нормальному с математическим ожиданием 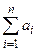и дисперсией 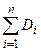. (Без доказательства).

Замечание 1. Неограниченное приближение закона распределения суммы 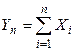к нормальному закону при 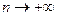означает, что 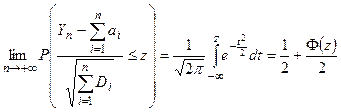, где 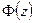– функция Лапласа.

Замечание 2. Смысл условия 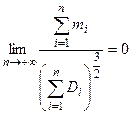состоит в том, чтобы в сумме 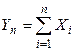не было слагаемых, влияние которого на рассеяние 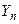подавляюще велико по сравнению с влиянием всех остальных, а также не должно быть большого числа слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных.

Центральная предельная теорема теории вероятностей объясняет, почему нормально распределённые случайные величины широко распространены. Для практики важно следующее

Следствие. Если , , 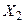…, 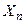–независимые одинаково распределённые случайные величины, у каждой из которых существует математическое ожидание 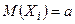, дисперсию 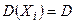, абсолютный центральный момент третьего порядка 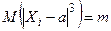, то закон распределения суммы 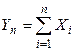при 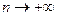неограниченно приближается к нормальному.

Доказательство. Так как 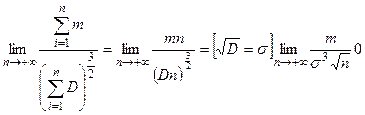, то выполняются все условия теоремы Ляпунова. Следовательно, закон распределения суммы 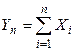при 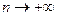неограниченно приближается к нормальному.

Замечание 1. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждого из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Замечание 2. Скорость сходимости суммы 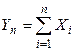к нормальному закону при 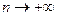существенно зависит от типа распределения слагаемых. На основании центрально предельной теоремы можно утверждать, что законы распределения биномиальный, Пуассона и другие, которые будут изучены позднее (распределение Стьюдента, хи-квадрат распределение), при 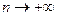распределены асимптотически нормально.