Свойство 1. 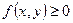 .
.
Доказательство следует из того, что 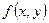 есть предел отношения неотрицательной величины к положительной величине:
есть предел отношения неотрицательной величины к положительной величине:
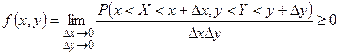 .
.
Или из того, что 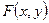 – неубывающая функция своих аргументов.
– неубывающая функция своих аргументов.
Свойство 2. Вероятность попадания двумерной случайной величины 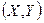 в область
в область 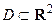 равна
равна 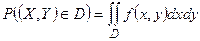 . (22.2)
. (22.2)
Доказательство. Согласно формуле (22.1) для любой точки 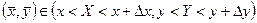 имеем право записать приближенное равенство для значения вероятности попадания в прямоугольник
имеем право записать приближенное равенство для значения вероятности попадания в прямоугольник 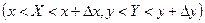 :
: 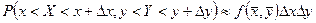 .
.
Пусть произвольная область 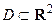 . Обозначим событие, состоящее в попадании случайной точки
. Обозначим событие, состоящее в попадании случайной точки 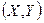 в область D, так:
в область D, так: 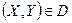 .
.
Разобъём область 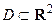 прямыми, параллельными осям координат на п прямоугольников со сторонами
прямыми, параллельными осям координат на п прямоугольников со сторонами 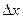 и
и 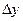 . Для простоты будем полагать, что эти прямые пересекают границу области D не более, чем в двух точках. Так как события, состоящие в попадании случайной точки
. Для простоты будем полагать, что эти прямые пересекают границу области D не более, чем в двух точках. Так как события, состоящие в попадании случайной точки 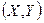 в прямоугольники
в прямоугольники 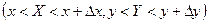 , несовместны, то вероятность попадания в область D может быть приближённо выражена формулой:
, несовместны, то вероятность попадания в область D может быть приближённо выражена формулой:
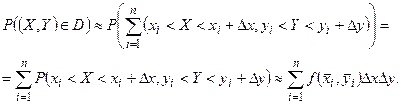
Переходя к пределу при 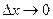 и
и 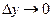 , получим
, получим 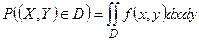 .
.
Замечание 4. Геометрически равенство (22.2) можно истолковать так: вероятность попадания случайной точки 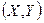 в область D равна объёму тела, ограниченного сверху поверхностью плотности распределения
в область D равна объёму тела, ограниченного сверху поверхностью плотности распределения 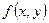 , основанием которого является проекция этой поверхности на плоскость ОХУ.
, основанием которого является проекция этой поверхности на плоскость ОХУ.
Замечание 5. Выражение 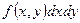 называют элементом вероятности. Элемент вероятности определяет вероятность попадания случайной точки в элементарный прямоугольник со сторонами
называют элементом вероятности. Элемент вероятности определяет вероятность попадания случайной точки в элементарный прямоугольник со сторонами 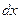 и
и 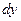 .
.
Свойство 3. Интегральная функция распределения непрерывной двумерной случайной величины может быть выражена через её плотность вероятности 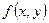 по формуле:
по формуле: 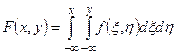 . (22.3)
. (22.3)
Доказательство непосредственно следует из определения дифференциальной функции распределения.
Свойство 4. 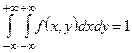 .
.
Доказательство. Двойной несобственный интеграл 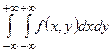 есть вероятность попадания случайной точки
есть вероятность попадания случайной точки 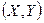 в
в 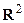 . Событие
. Событие 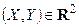 является достоверным. Поэтому
является достоверным. Поэтому 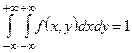 .
.
 2014-02-02
2014-02-02 691
691








