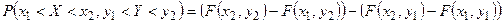 . (21.1)
. (21.1)
Доказательство. Так как событие попадания в полуполосу 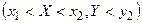 можно представить в виде суммы несовместных событий
можно представить в виде суммы несовместных событий 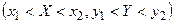 и
и 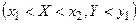 :
: 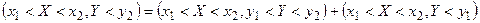 , тогда
, тогда 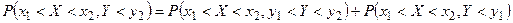 . Следовательно,
. Следовательно,
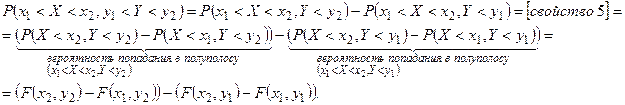
Замечание 4. Геометрически функция распределения двумерной случайной величины есть некоторая поверхность в пространстве 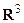 , обладающая указанными свойствами. Для дискретной двумерной случайной величины её функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции
, обладающая указанными свойствами. Для дискретной двумерной случайной величины её функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции 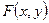 .
.
 2014-02-02
2014-02-02 671
671








