2014-02-02
1328
Плотность распределения вероятностей непрерывной двумерной случайной величины
Определение 1. Двумерная случайная величина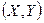 
называется непрерывной, если её функция распределения 
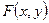– непрерывная функция, дифференцируемая по каждому из аргументов в 
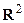, и всюду (за исключением, может быть, конечного числа кривых) имеет вторую смешанную производную 
.
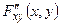Следствие.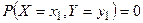 
.
Доказательство следует из формулы (21.1) пр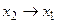и 
и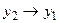 
с учётом непрерывности функции распределения .
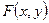Замечание 1. Согласно формуле (21.1) вероятность попадания случайной точки 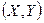в прямоугольник со сторонам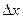и 
и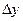 
будет равна:
.
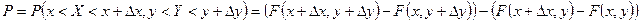Средняя плотность вероятности в данном прямоугольнике будет равна:
.
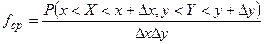Переходя к пределу пр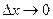и 
и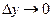 
, получим
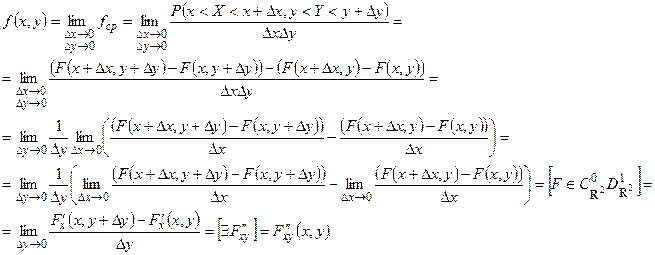
Определение 2. Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины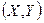 
называется вторая смешанная частная производная её функции распределения: 
.
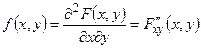Замечание 2. Геометрически плотность вероятности двумерной случайной величины 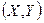представляет собой поверхность распределения в пространстве 
.
|
|
|
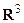Замечание 3. Согласно замечанию 1, функцию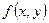 
можно рассматривать как предел отношения вероятности попадания случайной точки 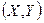в прямоугольник со сторонам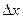и и 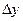к площади этого прямоугольника, когда обе стороны прямоугольника стремятся к нулю: 
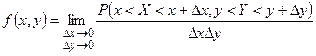. (22.1)
