Условные законы распределения составляющих системы непрерывных случайных величин

Определение 3. Условным законом распределения одной из одномерных составляющих двумерной случайной величины 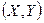называется её закон распределения, вычисленный при условии, что другая составляющая приняла определённое значение (или попала в определённый интервал).

Определение 4. Условной дифференциальной функцией 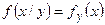составляющей Х при данном значении 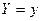называют отношение дифференциальной функции 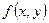системы случайных величин к дифференциальной функции 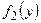составляющей У: 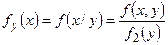. (22.4)

Замечание 6. В отличие от безусловной дифференциальной функции 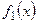составляющей Х, условная дифференциальная функция 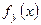даёт распределение случайной величины Х при условии, что составляющая У приняла значение .

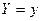Определение 5. Условной дифференциальной функцией 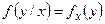составляющей У при данном значении 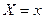называют отношение дифференциальной функции 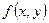системы случайных величин к дифференциальной функции 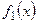составляющей Х: 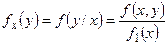. (22.5)

Замечание 7. Если известна дифференциальная функция 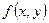системы случайных величин, то условные дифференциальные функции составляющих могут быть найдены в силу (28.4) и (28.5) по формулам: 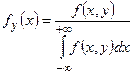и 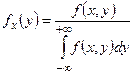. Как обычные дифференциальные функции, условные дифференциальные функции обладают свойствами:

1) 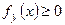, 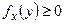. 2) , .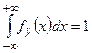

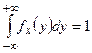Замечание 8. Соотношения (28.4) и (28.5) можно переписать в виде:

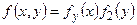и 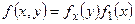. (22.6)

Соотношения (22.6) называют теоремой умножения плотностей распределений.