Свойство 1. 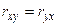 .
.
Доказательство следует из определения 5 и равенства 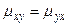 .
.
Свойство 2. Если случайные величины Х и У независимы, то 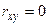 .
.
Доказательство следует из того, что для независимых случайных величин 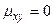 .
.
Свойство 3. Для любых случайных величин Х и У 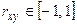 .
.
Доказательство. Так как 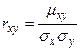 , а
, а 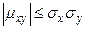 , то
, то 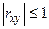 . Следовательно,
. Следовательно, 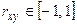 .
.
Свойство 4. 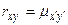 .
.
Доказательство. 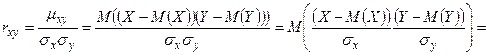
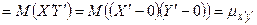 .
.
Свойство 5. Если 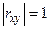 , то случайные величины Х и У связаны линейной функциональной зависимостью.
, то случайные величины Х и У связаны линейной функциональной зависимостью.
Доказательство. Рассмотрим случайные величины Х и У, соответствующие им нормированные случайные величины 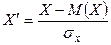 и
и 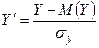 , и случайные величины
, и случайные величины 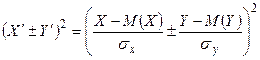 . Очевидно, что случайные величины
. Очевидно, что случайные величины 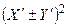 принимают только неотрицательные значения, следовательно, для их математических ожиданий справедливо неравенство (см. доказательство свойства 5 для корреляционного момента):
принимают только неотрицательные значения, следовательно, для их математических ожиданий справедливо неравенство (см. доказательство свойства 5 для корреляционного момента):
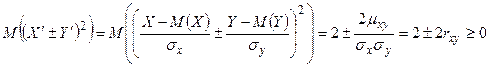 .
.
Если 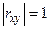 , то при
, то при 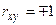 соответственно
соответственно 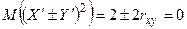 . Так как неотрицательные случайные величины
. Так как неотрицательные случайные величины 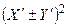 имеют математические ожидания, равные нулю, то, следовательно, и сами величины тождественно равны нулю:
имеют математические ожидания, равные нулю, то, следовательно, и сами величины тождественно равны нулю:
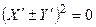 ,
, 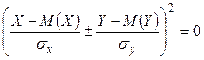 ,
, 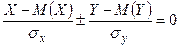 при
при 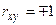 , или
, или
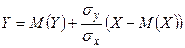 при
при 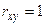 и
и 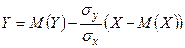 при
при 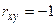 .
.
Т.е. Х и У связаны линейной функциональной зависимостью.
 2014-02-02
2014-02-02 1791
1791
