Определение1. Двумерная случайная величина 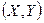 называется распределённой по двумерному нормальному закону, если её совместная плотность распределения имеет вид:
называется распределённой по двумерному нормальному закону, если её совместная плотность распределения имеет вид: 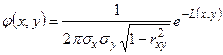 , где
, где 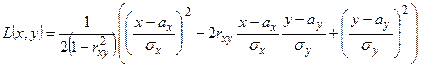 ,
,
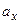 ,
, 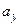 – математические ожидания случайных величин Х и У,
– математические ожидания случайных величин Х и У,
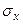 ,
, 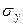 – средние квадратические отклонения случайных величин Х и У,
– средние квадратические отклонения случайных величин Х и У,
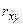 – коэффициент корреляции случайных величин Х и У.
– коэффициент корреляции случайных величин Х и У.
Замечание 1. Используя формулы § 22, можно убедиться, что каждый из законов распределения случайных величин Х и У является нормальным с параметрами соответственно 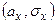 ,
, 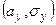 .
.
Замечание 2. Согласно § 22, условные плотности вероятности случайных величин Х и У имеют вид:
 ,
, 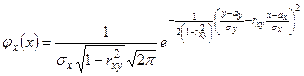
Можно убедиться в том, что каждый из условных законов распределения случайных величин Х и У является нормальным с условным математическим ожиданием и условной дисперсией, определяемыми по формулам:
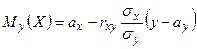 ,
, 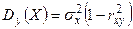 ,
, 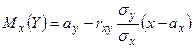 ,
, 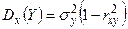 .
.
Из приведённых формул следует, что
1) линии регрессии 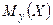 и
и 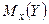 нормально распределённых случайных величин представляют собой прямые линии, т.е. нормальные регрессии У по Х и Х по У всегда линейны;
нормально распределённых случайных величин представляют собой прямые линии, т.е. нормальные регрессии У по Х и Х по У всегда линейны;
2) условные дисперсии  и
и 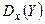 постоянны и не зависят от значений
постоянны и не зависят от значений 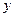 или
или 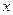 .
.
Теорема 1. Для нормально распределённых случайных величин понятия некоррелированность и независимость равносильны.
Доказательство. 1) Необходимость. Пусть случайные величины Х и У распределены нормально и некоррелированы. Тогда 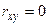 , и их совместная плотность распределения имеет вид:
, и их совместная плотность распределения имеет вид:
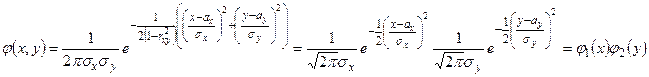 . По необходимому и достаточному условию независимости случайных величин, величины Х и У независимы.
. По необходимому и достаточному условию независимости случайных величин, величины Х и У независимы.
2) Достаточность. Если случайные величины независимы, то их корреляционный момент равен нулю, следовательно, они некоррелированы.
Замечание 3. Поверхность двумерного нормального распределения называют «палаткой Гаусса». Сечения этой поверхности плоскостями 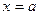 и
и 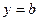 имеют форму нормальных кривых с центрами, лежащими на линии регрессии У по Х и Х по У, и со средними квадратическими отклонениями, равными
имеют форму нормальных кривых с центрами, лежащими на линии регрессии У по Х и Х по У, и со средними квадратическими отклонениями, равными 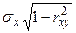 и
и 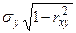 . Сечение поверхности нормального распределения плоскостью
. Сечение поверхности нормального распределения плоскостью 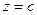 (
(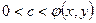 ), представляет собой эллипс, называемый эллипсом рассеяния:
), представляет собой эллипс, называемый эллипсом рассеяния: 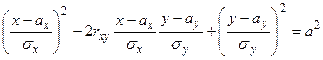 , где
, где  . Центр эллипса находится в точке
. Центр эллипса находится в точке 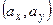 , а его оси образуют с осью Ох углы α и
, а его оси образуют с осью Ох углы α и 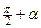 , где α определяется из условия
, где α определяется из условия 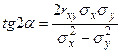 .
.
 2014-02-02
2014-02-02 2868
2868