Свойство 1. Математическое ожидание произведения двух любых случайных величин может быть вычислено по формуле: 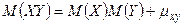 .
.
Доказательство. В силу свойства 4 корреляционного момента имеет место равенство: 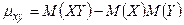 , тогда
, тогда 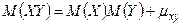 .
.
Следствие. Математическое ожидание двух некоррелированных случайных величин 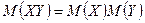 .
.
Доказательство следует из свойства 1 и того, что для некоррелированных случайных величин 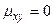 .
.
Замечание 10. Ранее это свойство было сформулировано и доказано только для независимых случайных величин. Теперь выясняется, что в случае двух случайных величин достаточно менее жёсткого требования некоррелированности случайных величин. В случае большего числа сомножителей требование независимости случайных величин должно быть сохранено.
Свойство 2. Дисперсия суммы двух любых случайных величин может быть вычислена по формуле: 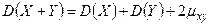 .
.
Доказательство. Пусть Z=Х+У. По свойству математического ожидания 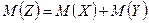 , поэтому
, поэтому 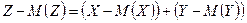 . По определению дисперсии
. По определению дисперсии
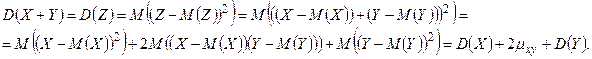
Замечание 11. Свойство может быть обобщено на любое число слагаемых: 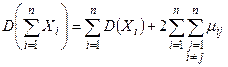 , где
, где 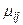 – корреляционный момент случайных величин
– корреляционный момент случайных величин 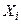 и
и 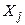 .
.
Замечание 12. Для некоррелированных и независимых случайных величин 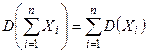 .
.
 2014-02-02
2014-02-02 1739
1739
