2014-02-02
8371
Определение 6. Две случайные величины Х и У называют коррелированными, если их корреляционный момент (или, что то же, - коэффициент корреляции) отличен от нуля.
Определение 7. Две случайные величины Х и У называют некоррелированными, если их корреляционный момент (или, что то же, - коэффициент корреляции) равен нулю.
Теорема 3. Если случайные величины Х и У коррелированны, то они и зависимы.
Доказательство. Вопреки утверждению допустим, что случайные величины независимы, тогда их корреляционный момент должен быть равен нулю, что противоречит условию, так как для коррелированных величин корреляционный момент отличен от нуля.
Замечание 9. Обратное утверждение не всегда имеет место, т.е. если две случайные величины зависимы, то они могут быть как коррелированными так и некоррелированными. Другими словами, корреляционный момент двух зависимых случайных величин может быть как равен, так и не равен нулю.
Пример. Двумерная случайная величина задана плотностью распределения: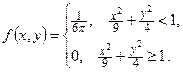 
Доказать, что Х и У зависимые некоррелированные случайные величины.
|
|
|
Решение. 1) Найдём дифференциальные функции составляющих:
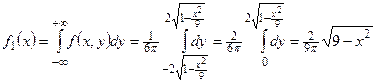, тогда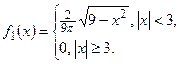 
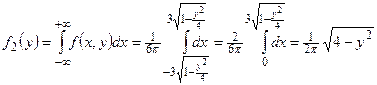, тогда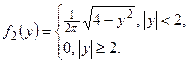 
2) Так как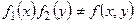 
, то Х и У зависимые случайные величины (по следствию к теореме 1).
3) Убедимся, что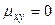 
. Так как функция 
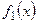симметрична относительно оси Оу, то 
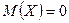. Аналогично, функция 
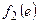симметрична относительно оси Ох, то 
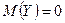. Тогда корреляционный момент равен:
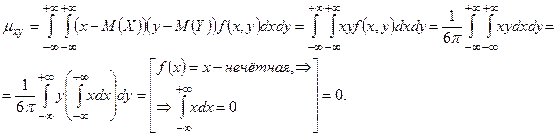
Таким образом, зависимые случайные величины некоррелированы.
Вывод. Из коррелированности случайных величин следует их зависимость, но из зависимости ещё не следует коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности не следует их независимость.
