Момент импульса. Основное уравнение динамики вращательного движения. Закон сохранения момента импульса

Мы уже отмечали аналогию между законами поступательного и вращательного движений, когда рассматривали кинематику. Но эта аналогия распространяется и на динамику. Так, аналогом импульса для вращательного движения служит величина, которая называется моментом импульса.

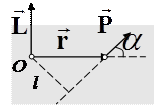
Рисунок 3.1 – Момент импульса частицы относительно точки О

Моментом импульса частицы относительно некоторой точки О называют вектор 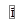, равный векторному произведению радиус-вектора, проведенного из точки О в точку приложения импульса, на импульс (рис. 3.1):

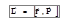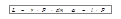, , (3.14)

где величина 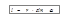и называется плечом вектора 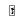относительно точки О.

Выясним, какая физическая величина определяет изменение вектора момента импульса. Для этого найдем производную по времени от вектора: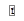

. (3.15)

Первое слагаемое в уравнении (3.15) тождественно равно нулю как векторное произведение двух коллинеарных векторов. Второе слагаемое в (3.15) называется моментом силы, и это есть векторное произведение радиус-вектора, проведенного в точку приложения силы, на эту силу (рис. 3.2):

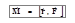. (3.16)

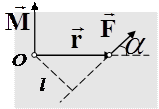
Рисунок 3.2 – Момент силы частицы относительно точки О

В результате для скорости изменения момента импульса мы получим так называемое уравнение моментов:

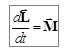. (3.17)

Производная по времени от момента импульса частицы относительно некоторой точки О равна моменту равнодействующей силы относительно той же точки О.

Теперь рассмотрим систему частиц. Сразу же отметим, что момент импульса – величина аддитивная. Это значит, что момент импульса системы частиц относительно некоторой точки О равен сумме моментов импульса отдельных частиц системы относительно той же точки О: 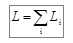. Тогда для системы частиц можно записать:

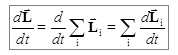. (3.18)

Теперь учтём, что на каждую i – ю частицу системы действуют как внутренние силы 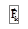со стороны других частиц системы, так и результирующая внешних сил 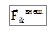. Тогда изменение момента импульса каждой частицы системы описывается уравнением

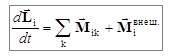, (3.19)

где .

Изменение результирующего момента импульса всей системы будет, очевидно, равно

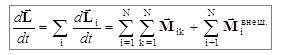. (3.20)

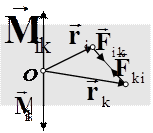
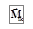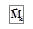Рисунок 3.3 – Моменты сил и частицы относительно точки О

Покажем, что двойная сумма в выражении (3.20) тождественно равна нулю (рис. 3.3). В самом деле:

. (3.21)

А так как моменты в двойной сумме встречаются попарно, то они взаимно уничтожаются. В выражении (3.21) мы учли, что на основании 3-го закона Ньютона 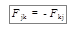. В выражении (3.20) заменим сумму моментов внешних сил результирующим, или главным моментом внешних сил относительно той же точки О: 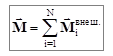. Тогда, в результате всех преобразований получим основной закон динамики для тела, вращающегося относительно неподвижной точки:

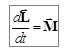. (3.22)

Скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту относительно той же точки всех внешних сил, действующих на систему. Если система замкнута, т.е. 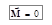, то 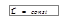. Или момент импульса замкнутой системы не изменяется с течением времени. Закон сохранения момента импульса является одним из фундаментальных законов природы. Его область применения гораздо шире, чем область применения классической механики, в рамках которой мы его получили. В теоретической физике доказывается, что он является следствием изотропии пространства. Изотропия пространства означает, что в пространстве нет выделенных направлений. Другими словами, поворот механической системы как целого на произвольный угол не изменяет свойства системы и законы её движения.