Момент инерции твердого тела. Теорема Штейнера

Момент инерции – очень важная характеристика вращающегося тела. Из основного закона динамики вращающегося тела (4.9) видно, что момент инерции описывает инертность тела во вращательном движении. Как и при поступательном движении, вращающееся тело “сопротивляется” изменению своей угловой скорости при действии момента сил[5]. Следовательно, момент инерции есть мера инертности твердого тела при вращательном движении.

Отметим некоторые свойства момента инерции, отличающие его от массы. Во-первых, момент инерции зависит от геометрических размеров тела. Это свойство момента инерции демонстрирует фигурист на льду, когда, прижимая руки к телу, он уменьшает свой момент инерции, что приводит к увеличению скорости вращения спортсмена в соответствии с законом сохранения момента импульса (4.10). Во-вторых, значение момента инерции зависит от выбора оси, относительно которой он вычисляется.

Момент инерции представляет собой, таким образом, важную величину, и нужно уметь определять её относительно произвольной оси вращения. Отметим, что в определении момента инерции (4.8) вычисления будут тем более точными, чем на большее число материальных точек можно разбить сумму в выражении (4.8). В пределе это означает переход к интегрированию:

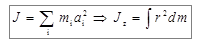. (4.11)

В формуле (4.11) r – это расстояние от выделенного элемента тела массой dm до оси вращения.

В качестве примера вычислим момент инерции однородного диска радиуса R относительно оси, перпендикулярной плоскости диска и проходящей через его центр. Выделим на диске кольцевой слой толщиной dr. Все точки этого слоя будут находиться на одинаковом расстоянии r от оси вращения, и выражение под знаком интеграла запишется в виде

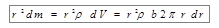. (4.12)

где r – плотность материала диска, b – толщина диска (рис. 4.3).

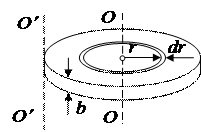
Рисунок 4.3 – Однородный диск радиуса R

Подставим выражение (4.12) в выражение (4.11) и проинтегрируем по r. В результате получим:

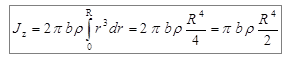. (4.13)

Теперь учтём в выражении (4.13), что масса всего диска равна произведению плотности r на объём диска bp R², и окончательно получим:

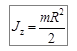. (4.14)

Вычислить момент инерции тела относительно произвольной оси, даже не проходящей через тело, позволяет теорема Штейнера, согласно которой момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

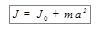. (4.15)

Вычислим момент инерции того же диска относительно оси O¢O¢, проходящей через образующую диска (рис. 4.3). В соответствии с теоремой Штейнера, момент инерции диска относительно оси O¢O ¢ будет равен

.

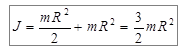Отметим, что прямое вычисление момента инерции диска относительно оси O¢O¢ по формуле (4.11) представляет собой более трудную задачу, чем та, которую мы решили.