Механическая работа. Мощность

ЭНЕРГИИ

ЛЕКЦИЯ 5. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ

Пусть частица под действием силы 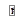движется по некоторой траектории из точки 1 в положение 2 (рис. 5.1). В общем случае сила 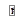может изменяться как по величине, так и по направлению.

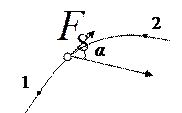
Рисунок 5.1 – Движение частицы под действием силы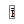

Рассмотрим элементарное перемещение 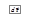, в пределах которого силу 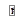можно считать постоянной. Элементарной работой dA силы 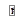на перемещении называют величину, равную скалярному произведению :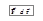

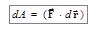, или 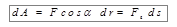, (5.1)

где 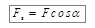– проекция силы 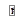на направление движения, 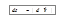. Работа dA – величина алгебраическая. Если угол 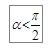, то работа положительная, если , то работа отрицательная. При 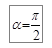работа тождественно равна нулю. Работа измеряется в джоулях (Дж). Размерность работы – [Дж] = Н∙м. Работа, совершаемая на конечном пути s, равна сумме элементарных работ на отдельных участках ds или интегралу

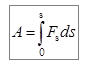. (5.2)

Работе можно придать наглядный геометрический смысл. Если сила F _s задана как функция пройденного пути s, то работа на этом пути равна площади ограниченной кривой 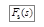в координатах s и F _s(рис. 5.2).

Рисунок 5.2 – Работа

Если на частицу одновременно действуют несколько сил, то работа результирующей силы равна алгебраической сумме работ, совершаемых каждой из сил на том же перемещении:

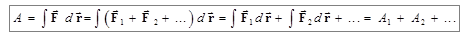
Величина, характеризующая скорость выполнения работы силой 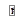, и равная работе, произведенной в единицу времени, называется мощностью:

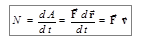. (5.3)

Величина мощности в системе СИ измеряется в ваттах (Вт), и [Вт]=Дж/с. Мы также знаем ещё одну единицу измерения мощности – лошадиная сила: 1 л.с. = 736 Вт.