Две плоскости пересекаются по прямой линии, для определения которой достаточно найти две точки, принадлежащие одновременно каждой из заданных плоскостей. Для нахождения этих точек достаточно ввести две вспомогательные секущие плоскости, занимающие проецирующее положение (см. рис. 6.1).
Рис. 6.1
Задача по нахождению точки встречи прямой с плоскостью сводится к задаче по определению линии пересечения исходной плоскости со вспомогательной плоскостью, занимающей проецирующее положение и содержащей в себе заданную прямую. Точка встречи - это точка пересечения полученной линии и заданной. Затем при помощи конкурирующих точек определяется видимость участков проекций заданной прямой (см. рис. 6.2). Можно утверждать, что в плоскости треугольника есть прямая
линия 1, 2, горизонтальная проекция которой совпадает с горизонтальной прямой l.
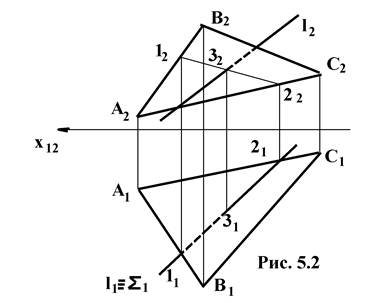
Рис. 6.2
 2014-02-02
2014-02-02 749
749







