Две поверхности пересекаются по линии, точки которой принадлежат каждой из пересекающихся поверхностей.
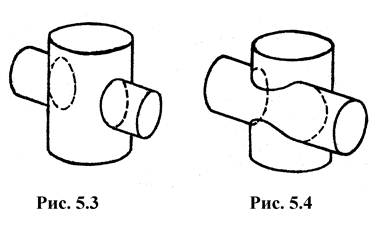
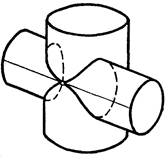
Рис. 6.3 Рис. 6.4 Рис. 6.5
ПОЛНОЕ ПЕРЕСЕЧЕНИЕ (рис. 6.3) - все образующие одной поверхности пересекают все образующие другой поверхности. В результате получаются двезамкнутые ветви пространственной линии.
НЕПОЛНОЕ ПЕРЕСЕЧЕНИЕ (рис. 6.4) - часть образующих одной поверхности пересекается с частью образующих другой поверхности. При этом получается одна замкнутая пространственная линия пересечения.
ОДНОСТОРОННЕЕ КАСАНИЕ (рис. 6.5) - Одна образующая поверхности расположена касательно к другой поверхности. При этом получается замкнутая пространственная кривая линия с самопересекающимися ветвями в точке касания.
ОСОБЫЕ СЛУЧАИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА
Две поверхности второго порядка в общем случае пересекаются по кривым четвертого порядка. Однако в некоторых особых случаях поверхности второго порядка могут пересекаться по двум плоским кривым второго порядка. Рассмотрим эти случаи.
1. Если две поверхности второго порядка пересекаются по одной плоской кривой второго порядка, то они пересекаются еще по одной плоской кривой второго порядка. На рис. 6.6 показан пример пересечения конуса вращения с круговым наклонным цилиндром. В пересечении этих фигур получаются две плоские кривые - эллипс AB и окружность DE.
Любая плоская кривая, лежащая на поверхности второго порядка, есть кривая второго порядка. Поэтому, если пространственная кривая четвертого порядка распадается на две кривые и одна из них линия второго порядка, то вторая кривая будет плоской кривой второго порядка.
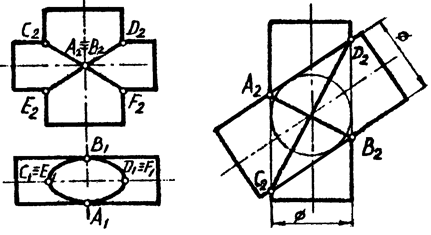
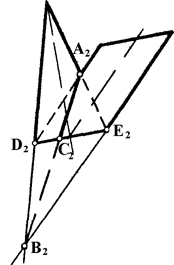
Рис. 6. 6 Рис. 5.7 Рис. 6.8
2. Если две поверхности второго порядка касаются в двух точках, то линия их пересечения распадается на две плоские кривые второго порядка. На рис. 6.7 приведен пример пересечения кругового и эллиптического цилиндров, имеющих две точки касания Aи B. В пересечении этих фигур получаются два эллипса - CFи DE,проходящие через точки A и B.
3. Теорема Г.Монжа
Если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то линия их пересечения распадается на две плоские кривые второго порядка. На рис. 6.8 приведен пример пересечения двух цилиндров, описанных около одной сферы. В пересечении получаются два эллипса AB и CD.
Эта теорема часто встречается на практике.
 2014-02-02
2014-02-02 3720
3720
