Пересечение двух поверхностей

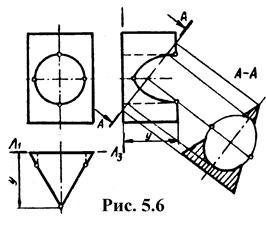
Рассмотрим пример построения линии пересечения прямой треугольной призмы, занимающей горизонтально проецирующее положение, со сквозным цилиндрическим отверстием, поверхность которого занимает фронтально проецирующее положение (рис. 6.18).

Рис. 6.18

Данное пересечение является полным. Образуются две замкнутые ветви линий пересечения: передняя состоит из двух ветвей эллип­сов, а задняя - окружность. Две проекции искомых линий пересечения на чертеже заданы их фронтальными проекциями, совпадающими с вырожден­ной проекцией поверхности цилиндра, а горизонтальные - находятся на вырожден­ной проекции призмы. Профильную прое­кцию фигуры и линии пересечения строят координатным методом.

ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР, ОДНА ИЗ КОТОРЫХ ЗАНИМАЕТ ПРОЕЦИРУЮЩЕЕ ПОЛОЖЕНИЕ, А ДРУГАЯ – НЕПРОЕЦИРУЮЩЕЕ

В этом случае только одна проекция общего элемента совпадает с вырожденной проекцией одной из пересекаемых фигур (проецирующей). Вторая проекция искомого общего элемента определяется из условия принадлежности его к не проецирующей поверхности фигуры.

Пример построения линии пересечения прямого кругового конуса с треугольным призматическим отверстием, поверх­ность которого занимает фронтально проецирующее положение (рис. 6.19).

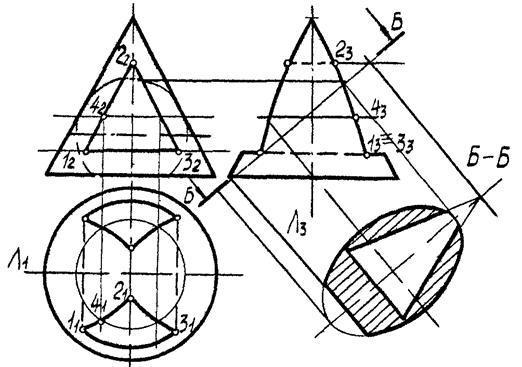Рис. 6.19

В данном случае пересечение является полным и дает две замкнутые ветви линии пересечения, каждая из которых состоит из двух дуг парабол и дуги окружности. Одна проекция искомой линии пересечения на чертеже совпадает с выраженной фрон­тальной проекцией призматического отверстия.

Отметим фронтальные проекции характерных точек линий пересечения (точки из лома-1₂ , 2₂, 3₂) и проекцию промежуточной точки 4₂ .

Горизонтальные проекции 1₁, 2₁,3₁, 4₁ этих точекстроятся по условию их принадлежности к поверхности конуса (вспомогательная окружность) и соединяются плавными кривыми линиями.Профильную проекцию фигуры и линии пересечения строят координатным методом. Построим также натуральную величину сечения Б – Б фигуры профильно-проецирующей плоскостью. В сечении конуса получается усеченный эллипс, а в сечении призмы треугольник. Искомое сечение состоит из этих двух простых сечений.