Способ эксцентрических сфер

Данный способ применяется при пересечении поверхностей вращения и циклических поверхностей, имеющих общую плоскость симметрии и состоит в применении вспомогательных сфер, имеющих различные центры. Заданные поверхности должны содержать семейства окружностей, по которым их могут пересе­кать эксцентрические сферы, общие для этих поверхностей.

.

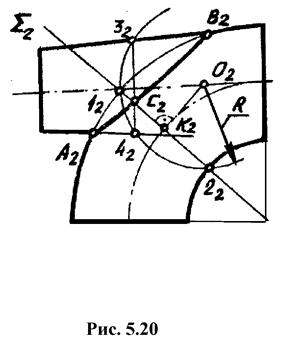
Рис. 6.24

На рис. 6.24 рассмотрен пример построения линии пересечения поверхности тора с конической поверхностью вращения, имеющих фронтальную плос­кость симметрии

Отмечаем точки A₂ и B₂ пересечения контуров поверх­ностей тора и конуса на фронтальной проекции. Через центр вращения тора проведем несколько фронтально-проецирующих плос­костей, каждая из которых пересекает тор по окружности, например:

1. Проводится плоскость S через центр тора. S пересекает поверхность тора по окружности 1-2. На фронтальной проекции она вырождается в прямую.

2. Из центра окружности 1-2 (точка К₂) проводится касательная к проекции осевой окружности тора до пересечения с осью конуса (точка О₂).

3. Из точки О₂ радиусом R проводится сфера-посредник, которая в пересечении конуса и тора даёт окружности 1-2 и 3-4, проецируемые в прямые.

4. Отмечается точка С пересечения окружностей 3-4 и 1-2, принадлежащую одновременно двум пересекаемым поверхностям.

5. Действия повторяют для других плоскостей.