Способ концентрических сфер

Рис. 6.20

ПЕРЕСЕЧЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР, ЗАНИМАЮЩИХ ОБЩЕЕ ПОЛОЖЕНИЕ

В данном случае на чертеже нет проекций искомого общего элемента. Для решения задачи применяют вспомогательные секу­щие поверхности-посредники.

1. Пересечение линии с поверхностью

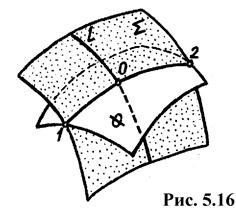
Дано: поверхность Φи линия l, пересекающая эту поверхность (рис. 5.16).

Алгоритм решения данной задачи заключается в следующем.

1. Через линию l проводим поверхность посредник S;

2. Строим линию пересечения заданной поверхности Φ с посредником S

(1-2 = S Ç l);

3. Находим точку O, как результат пересечения исконной линии и линии пересечения 1-2

(О = 1-2 Ç l);

4. Определяем видимость фигур.

Особое значение имеет правильный выбор посредника, который состоит в том, чтобы при пересечении его с заданной поверхностью получались графически простые линии – прямые или окружности.

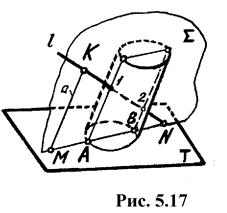
В случае приведенням на рис. 5.17 посредником целесообразно выбирать плоскость об­щего положения, проходящую через данную прямую и параллельную об­разующим цилиндра. Для этого через произвольную точку K проведем прямую l, параллельную образующим цилиндра, и построим след MN этого посредника. Затем отметим точки A и B и про­ведем две образующие, полученные в результате пересечения посред­ника с поверхностью цилиндра. Находим искомые точки I и 2 пересе­чения прямой l с поверхностью данного цилиндра.

2. Пересечение поверхностей общего вида

Для построения линии пересечения непроецирующих поверхнос­тей применяют метод вспомогательных секущих поверхностей-посредни­ков, которыми обычно служат плоскости или сферы, пересекающие данные поверхности по прямым линиям или окружностям.

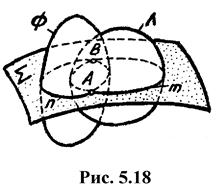
Рис. 6.21

Решение подобных задач в общем случае, приведенном на рис. 6.21, заклю­чается в следующем.

1. Проводим поверхность посред­ник Σ.

2. Строим линии пересечения n и m посредника Σ с поверхностями Φ и Λ

(n = F Ç L, m = L Ç S).

3. Находим общие точки пересечения полученных линий

(A = n Ç m,B = n Ç m.). Точки A и B являются точками двойной принадлежности.

4. Повторяем аналогичные построения с другими посредниками.

5. Соединяем полученные точки с учетом их видимости.

Способ вспомогательных плоскостей уровня

Рис. 6.22

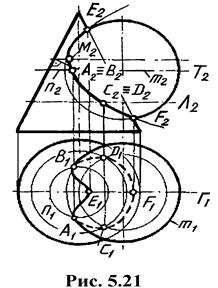
На рис. 6.22 рассмотрен пример построения линии пересечения конуса и сферы.

Посредниками целесообраз­но выбрать плоскости уровня, параллельные Π ₁, которые бу­дут пересекать обе данные поверх­ности по окружностям. Плоскость Τ (Τ ₂), проходя через центр сферы и пересекая тела, образует в пересечении окружности m(m ₁, m ₂) и n(n ₁, n ₂). Результатом пересечения этих окружностей являются опорные точки A (A ₁, A ₂) и B(B ₁, B ₂). Их горизонтальные проекций определяют границы видимости линии пересечения на плоскости П ₁. Вспомогательная плоскость Λ(Λ2)

определяет следующую пару промежуточных точек C(C ₁, C ₂) и D(D ₁, D ₂) и так далее.

Плоскость Γ(Γ ₁) параллельна плоскости Π ₂ и сов­падает с плоскостью симметрии дан­ных фигур. Она пересекает конус по треугольнику, а сферу - по ок­ружности, которые на фронтальной проекции изображаются очерковыми образующими и дают две экстремальные точки E(E ₁, E ₂) и F(F ₁, F ₂). Соединив полученные точки плавной кривой, получим искомую линию пересечения, Отметим, что фронтальная проекция искомой линии пересечения имеет вид параболы с вершиной M.

служат две плоскости уровня Т и А *' -

Этот способ применяется при построении линии пересечения поверхностей вращения, оси которых пересекаются и параллельны од­ной из плоскостей проекции.

В основу данного способа положено свойство сферы с центром на оси какой-либо поверхности вращения, пересекать эту поверхность по окружности. При этом если ось поверх­ности вращения параллельна плоскости проекций, то окружности прое­цируются на эту плоскость в отрезки прямых.

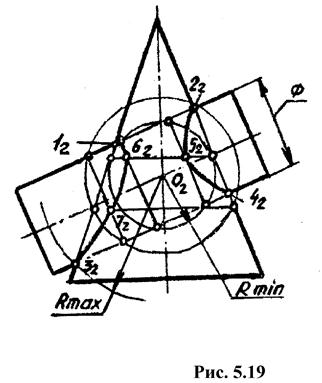
Рис. 6.23

На рис. 6.23 рассмотрен пример построения линии пересечения цилиндра и конуса вращения, оси которых пересека­ются в точке О (O₂) и параллельны плоскости проекций Π ₂ . Вначале отметим точки пересечения очер­ковых образующих. Затем помещаем центры вспомогательных сфер в точку пересечения осей O₂ и строим вырожденные проекции окружностей как линии пересечения вспомогательных сфер с поверхностями конуса и цилиндра. Точки пересече­ния фронтальных проекций этих окружностей (5 ₂, 6 ₂, 7 ₂) принадлежат искомой линии пересечения. Отметим, что фронтальная проекция линии пересечения в данном случае имеет вид гиперболы.