2014-02-03
983
Понятие о политропных процессах в идеальном газе
Расчёт процессов базируется на первом и втором началах термодинамики, которые мы запишем в дифференциальной форме для одного килограмма термодинамической системы. Пересчёт на всю массу системы будет осуществляться простым умножением удельных характеристик системы на ее массу М.
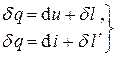- I начало термодинамики, (3.17)
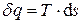- II начало термодинамики. (3.18)
Входящие в эти выражения дифференциалы вычисляются следующим образом:
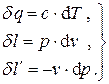(3.19)
Кроме того, для идеального газа имеем
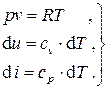(3.20)
Считается также заданной химическая формула газа или, в случае смеси, её состав, т.е. считаются заданными величины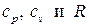 
.
С математической точки зрения система уравнений (3.17) – (3.20) является незамкнутой, т.к. девять уравнений содержат десять неизвестных. В качестве последнего, десятого, должно задаваться уравнение процесса, т.е. функциональная зависимость между параметрами системы, определяемая наложением внешних условий, связанных со свойствами оболочки, ограничивающей рассматриваемую термодинамическую систему.
|
|
|
На практике чаще всего имеют дело с термодинамическими процессами, в течение которых на каждых малых участках процесса можно с достаточной точностью считать постоянным соотношение между количествами работы и теплоты. Такие процессы называют политропными. Итак, по определению, для политропных процессов имеем:
Поскольку для идеального газа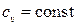 
, отсюда следует, что уравнение политропного процесса может быть записано в виде:
,
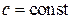т.е. политропный процесс можно определить как процесс с постоянной теплоёмкостью.
Соотношения между параметрами в политропном процессе можно получить на основании уравнений политропного процесса в переменных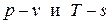 
. Используем для этого две записи I начала термодинамики в формах (3.17), подставив в них дифференциалы из (3.19) и (3.20):
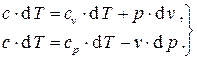(3.21)
Перенеся слагаемые с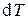 
в левые части этих выражений и разделив второе уравнение на первое, получим:
.
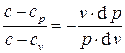Комплекс n (постоянный в случае политропного процесса):
; 
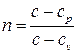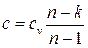; (3.22)
носит название показателя политропы, а с - теплоемкости политропного процесса. Имеем, таким образом:
.
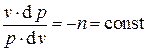Разделяя переменные в этом уравнении и интегрируя, получаем связь между давлением и объёмом в политропном процессе в виде:
.
.
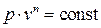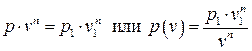Далее, получим уравнение политропного процесса в переменных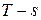 
. Из (3.2) и (3.3) имеем:
.
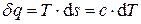Отсюда с учётом постоянства теплоёмкости легко получаем:
.
Используя начальные данные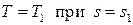 
, находим уравнение политропного процесса в координатах :
.
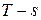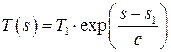соотношения между параметрами в политропном процессе:
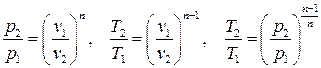
Вычисление количества теплоты в политропном процессе производится в соответствии с определением (1.32) или (1.33), т.е.:
|
|
|
.
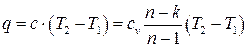выражение для удельной работы изменения объёма в трёх эквивалентных формах:
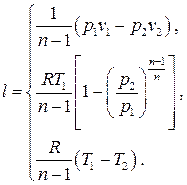
Полезная внешняя работа может быть вычислена
