2014-02-03
5784
Рассмотрим произвольный обратимый цикл теплового двигателя, изображённый на рис. 3.3. Его можно осуществить только в случае, если количество верхних и нижних источников тепла достаточно велико (в пределе бесконечно велико).
Такой произвольный цикл можно представить набором достаточно узких (в пределе бесконечно узких) циклов Карно, работающих при различных температурах верхних и нижних источников тепла.
 |
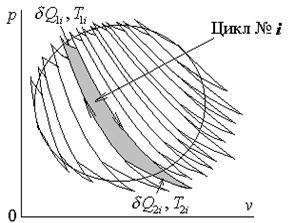Рис. 3.3.
Для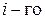 
цикла Карно имеем на основании (3.10):
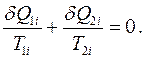
Суммируя это равенство по всем N циклам Карно, получим:
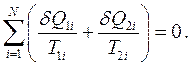
Переобозначив индексы, эту сумму можно переписать в виде:
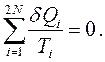
В пределе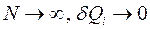 
эта сумма преобразуется в интеграл по замкнутому контуру (циклу)
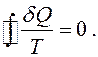(3.11)
Этот результат носит название интеграла Клаузиуса.
3.7. Неравенство Клаузиуса. Математическое выражение II начала термодинамики
Помимо цикла Карно, работающего в интервале температур верхнего источника тепла T 1 и нижнего источника тепла T 2 и имеющего, как мы выяснили, максимально возможный в данном интервале температур термический КПД, рассмотрим какой-либо другой цикл, функционирующий в том же интервале температур. Как следует из первой теоремы Карно, термический КПД такого цикла заведомо будет ниже термического КПД цикла Карно, а сам цикл заведомо будет необратимым. Имеем тогда неравенство
|
|
|
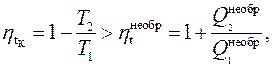
откуда следует, что сумма приведённых теплот для необратимого цикла отрицательна:
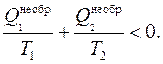(3.12)
Рассуждая аналогично тому, как мы это делали при выводе интеграла Клаузиуса (3.11), т.е. рассматривая произвольный необратимый цикл и разбивая его мысленно множеством адиабат на большое (в пределе бесконечное) число циклов с различными значениями Т 1 и Т 2, получим неравенство Клаузиуса
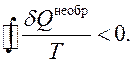(3.13)
Нуль в правой части этого неравенства есть не что иное, как интеграл по замкнутому контуру от дифференциала энтропии для обратимого цикла, т.е.
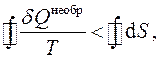
откуда, ввиду произвольности контура интегрирования, получаем
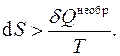(3.14)
Это неравенство говорит о том, что изменение энтропии вещества в любом необратимом процессе всегда больше приведённой теплоты этого процесса.
(3.15)
Результаты (3.11), (3.14) объединим в одной записи, которую можно считать математической формулировкой второго начала термодинамики:
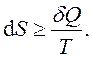(3.16)
Здесь знак (=) относится к обратимым процессам, а знак (>) – к необратимым.
