Рис.29
Рис.28
Рис.27
Сила 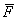 , как видим, стремится вернуть точку в равновесное положение О, где
, как видим, стремится вернуть точку в равновесное положение О, где 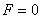 ; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.
; отсюда и наименование «восстанавливающая» сила. Примером такой силы является сила упругости. Коэффициент c пропорциональности называется жесткостью упругого элемента.
Найдем закон движения точки М. Составляя дифференциальное уравнение движения получим
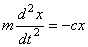 .
.
Деля обе части равенства на т и вводя обозначение
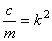 ,
,
приведем уравнение к виду
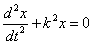 .
.
Уравнение представляет собою дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого линейного однородного дифференциального уравнения второго порядка ищут в виде x=ent. Полагая x=ent, получим для определения п так называемое характеристическое уравнение, имеющее в данном случае вид п2 + k2 = 0. Поскольку корни этого характеристического уравнения являются чисто мнимыми (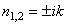 ), то, как известно из теории дифференциальных уравнений, общее решение имеет вид
), то, как известно из теории дифференциальных уравнений, общее решение имеет вид
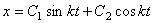 ,
,
где C 1 и С 2 - постоянные интегрирования. Если вместо постоянных C 1 и С 2 ввести постоянные а и 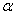 , такие, что
, такие, что 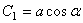 ,
, 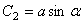 , то мы получим
, то мы получим 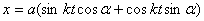 или
или 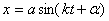 .
.
Это другой вид решения, в котором постоянными интегрирования являются а и 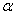 . Им удобнее пользоваться для общих исследований.
. Им удобнее пользоваться для общих исследований.
Скорость точки в рассматриваемом движении равна
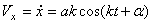 .
.
Колебания, совершаемые точкой по закону 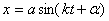 называются гармоническими колебаниями.
называются гармоническими колебаниями.
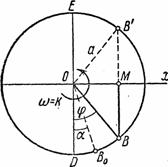
Всем характеристикам этого движения можно дать наглядную кинематическую интерпретацию. Рассмотрим точку В, движущуюся равномерно по окружности радиуса а из положения В 0 определяемого углом 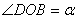 (рис.28).
(рис.28).
Пусть постоянная угловая скорость вращения радиуса ОВ равна k. Тогда в произвольный момент времени t угол 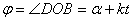 и проекция М точки В на диаметр, перпендикулярный к DE, движется по закону
и проекция М точки В на диаметр, перпендикулярный к DE, движется по закону 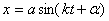 , где х=ОМ, т.е. совершает гармонические колебания.
, где х=ОМ, т.е. совершает гармонические колебания.
Величина а, равная наибольшему отклонению точки М от центра колебаний, называется амплитудой колебаний. Величина 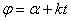 называется фазой колебаний.
называется фазой колебаний.
Величина k, совпадающая с угловой скоростью вращения радиуса ОВ, показанного на рис.15 называется круговой частотой колебаний.
Промежуток времени Т (или 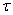 ), в течение которого точка совершает одно полное колебание, называется периодом колебаний.
), в течение которого точка совершает одно полное колебание, называется периодом колебаний.
По истечении периода фаза изменяется на 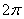 . Следовательно, должно
. Следовательно, должно 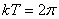 откуда период
откуда период
 .
.
Величина 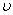 , обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний
, обратная периоду и определяющая число колебаний, совершаемых за одну секунду, называется частотой колебаний
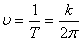 .
.
Отсюда видно, что величина k отличается от Т только постоянным множителем 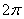 . В дальнейшем мы обычно для краткости частотой колебаний будем называть величину k.
. В дальнейшем мы обычно для краткости частотой колебаний будем называть величину k.
Значения а и 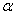 определяются по начальным условиям. Считая при t =0
определяются по начальным условиям. Считая при t =0 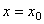 ,
, 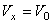 получим
получим 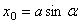 и
и 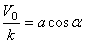 . Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:
. Отсюда, складывая сначала квадраты этих равенств,а затем деля их почленно, найдем:
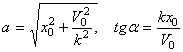 .
.
Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами: 1) амплитуда и начальная фаза колебаний зависят от начальных условий; 2) частота k, а следовательно, и период Т колебаний от начальных условий не зависят.
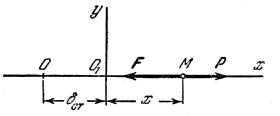
Влияние постоянной силы на свободные колебания точки. Пусть на точку М, кроме восстанавливающей силы F, направленной к центру О, действует еще постоянная по модулю и направлению сила Р (рис.29). Величина силы F по прежнему пропорциональна расстоянию от центра О, т.е. 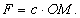
Очевидно, что в этом случае положением равновесия точки М будет центр О 1 отстоящий от О на расстоянии 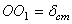 , которое определяется равенством
, которое определяется равенством 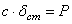 или
или
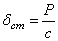 .
.
Величину 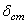 назовем статическим отклонением точки. Примем центр O 1 за начало отсчета и направим координатную ось О 1 х в сторону действия силы
назовем статическим отклонением точки. Примем центр O 1 за начало отсчета и направим координатную ось О 1 х в сторону действия силы 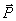 . Тогда
. Тогда 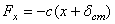 ,
, 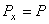 . В результате, составляя дифференциальное уравнение движения и учитывая, что согласно равенству
. В результате, составляя дифференциальное уравнение движения и учитывая, что согласно равенству 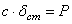 , будем иметь:
, будем иметь:
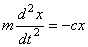 или
или 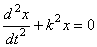 .
.
Отсюда заключаем, что постоянная сила Р не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силыF, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения 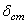 .
.
Обычное описание движения системы с одной степенью свободы в виде зависимости координаты от времени 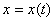 не является единственно возможным. В ряде случаев, особенно при изучении нелинейных механических колебаний, определенными достоинствами обладает представление движения на фазовой плоскости.
не является единственно возможным. В ряде случаев, особенно при изучении нелинейных механических колебаний, определенными достоинствами обладает представление движения на фазовой плоскости.
Состояние системы в любой фиксированный момент времени 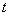 определяется парой соответствующих значений
определяется парой соответствующих значений 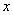 и
и  и может быть представлено изображающей (фазовой) точкой в плоской декартовой системе координат
и может быть представлено изображающей (фазовой) точкой в плоской декартовой системе координат 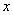 ,
, 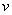 , если откладывать по оси абсцисс координату
, если откладывать по оси абсцисс координату 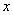 , а по оси ординат – скорость
, а по оси ординат – скорость 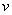 . Такая плоскость называется фазовой.
. Такая плоскость называется фазовой.
В процессе движения рассматриваемой системы величины 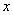 и
и 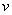 изменяются и, соответственно, меняется положение изображающей точки на фазовой плоскости. Геометрическое место изображающих точек для данного движения называется фазовой траекторией.
изменяются и, соответственно, меняется положение изображающей точки на фазовой плоскости. Геометрическое место изображающих точек для данного движения называется фазовой траекторией.
Для построения фазовой траектории при заданном законе движения 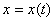 нужно путем дифференцирования образовать выражение скорости
нужно путем дифференцирования образовать выражение скорости 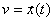 , а затем исключить время из двух уравнений:
, а затем исключить время из двух уравнений: 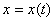 ,
, 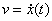 .
.
Функция 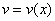 и описывает фазовую траекторию данного движения.
и описывает фазовую траекторию данного движения.
Фазовая плоскость особенно удобна для представления колебательных процессов, когда координата и скорость не выходят за известные пределы; поэтому вся картина движения даже в течение неограниченного времени занимает ограниченную часть фазовой плоскости.
Совокупность фазовых траекторий, которая описывает все возможные движения данной системы, называется фазовой диаграммой (фазовым портретом) данной системы.
Для свободных гармонических колебаний 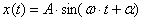 , а
, а 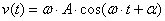 . Исключая из этих выражений время
. Исключая из этих выражений время 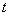 получаем
получаем
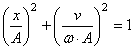 .
.
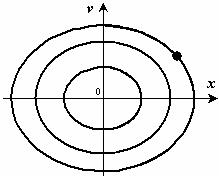
Это уравнение эллипса (рис.30). Его полуоси зависят от амплитуды и круговой частоты.
 2014-02-03
2014-02-03 709
709








