Вынужденные колебания с вязким сопротивлением

Рис.39

Рис.38

Рис.37

Рис.36

Свободные колебания с вязким сопротивлением.

Рис.35

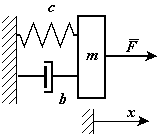
Существуют устройства (демпферы), которые создают силу пропорциональную относительной скорости 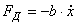(рис.36). Коэффициент пропорциональности называется коэффициентом демпфирования или коэффициентом вязкого сопротивления.

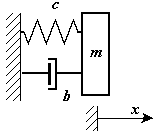
Дифференциальное уравнение движения точки с массой m, закрепленной на упругом элементе и демпфере имеет вид:

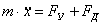
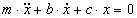или , , .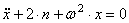

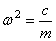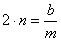Начальные условия имеют вид: , , .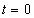

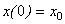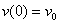Характеристическое уравнение имеет вид: .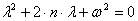

Корни характеристического уравнения равны: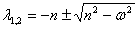

Рассмотрим возможные решения:

1-й случай , ,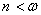

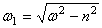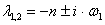
Решение имеет вид:

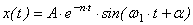
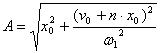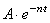, - условная амплитуда затухающих колебаний;

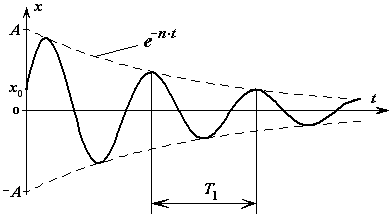
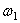- круговая или циклическая частота затухающих колебаний. Измеряется в рад/сек.

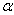- фазовый угол (или просто фаза).

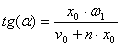
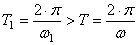- период затухающих колебаний (рис.37).

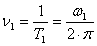- частота колебаний (1 колеб/cек=1 Гц)

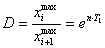- декремент колебаний.

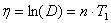- логарифмический декремент колебаний.

Материальная точка совершает гармонические колебания с частотой 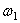и амплитудой, величина которой все время убывает.

Движение изображающей точки на фазовой плоскости показано на рис. 38.

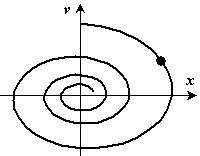
2-й случай , ,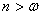

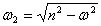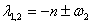
Решение имеет вид:

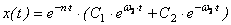
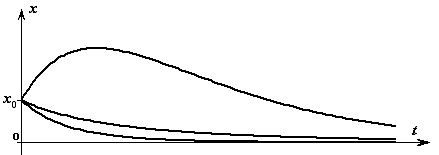
Материальная точка совершает затухающее неколебательное движение (рис.39).

3-й случай 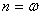, 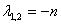(два одинаковых корня)

Решение имеет вид:

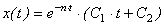
Материальная точка так же совершает затухающее неколебательное движение (рис.39).

Рассмотрим движение точки под действием трех сил: одна восстанавливающая сила, вторая - сила демпфирования (сила вязкого сопротивления), а третья зависит от времени. 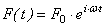- гармоническая возмущающая сила.

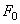- амплитуда возмущающей силы.

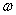- круговая частота возмущающей силы.