Классификация САР
Типовая функциональная схема САР
Система автоматического управления включает в себя ряд элементов, каждый из которых выполняет определённую функцию. Между элементами существуют физические взаимосвязи, которые удобно отображать схематически в какой-либо условной форме.
САУ может быть разделена на части по различным признакам: назначению частей, алгоритмам преобразования информации, конструктивной обособленности. Соответственно различают следующие структуры и структурные схемы САУ:
- функциональную;
- алгоритмическую;
- конструктивная.
Следует понимать, что структура – это совокупность связанных между собой частей чего-либо целого; структурная схема – это графическое изображение структуры.
В теории автоматического управления чаще всего имеют дело с функциональной схемой, поэтому она рассматривается более подробно.
Функциональная схема отражает функции (целевое назначение) отдельных частей САУ и состоит из условных изображений элементов и звеньев и различных связей в виде линий со стрелками, показывающих направление передачи воздействий. Каждая линия соответствует обычно одному сигналу или одному воздействию. В соответствии с ГОСТ 21.404-85 для составления функциональных схем используют следующие условные обозначения:
 | – преобразователь информации; прибор, установленный за щитом; |
 | – прибор, установленный на щите либо на пульте. |
Обозначение контролируемой величины осуществляется с помощью букв:
| D | – плотность; |
| E | – любая электрическая величина; |
| F | – расход; |
| G | – размер, положение, перемещение; |
| K | – время; |
| L | – уровень; |
| M | – влажность; |
| P | – давление, вакуум; |
| Q | – любая характеристика вещества (состав, концентрация и др.) |
| R | – радиоактивность; |
| S | – частота вращения |
| T | – температура; |
| V | – вязкость; |
| H | – масса; |
| W | – ручное действие; |
| U | – способность контролировать несколько величин. |
Другие величины обозначают резервными буквами A, B, C, N и др.; значение этих букв указывается непосредственно на схеме.
Характер контролированной величины уточняется с помощью дополнительных букв, которые ставятся после обозначения величины: D – разность; F – соотношение; Q – интегрирование, например:
 | – контроль разности температур; |
 | – контроль соотношения давлений; |
 | – контроль полного расхода жидкости либо газа. |
После обозначения контролированной величины указываются функциональные признаки. Для преобразователей: Е – первичное преобразование информации; Т – дополнительное преобразование информации для дистанционной передачи сигнала. Для приборов: I – показания; R – регистрация; C – управление, регулирование; S – наличие контактного прибора; A – сигнализация (H – верхней границы, L – нижней). Например:
 | – первичный преобразователь температуры; |
 | – вторичный преобразователь для дистанционной передачи информации о расходе вещества; |
 | – прибор за щитом для измерения температуры, показывающий и регистрирующий. |
По характеру изменения регулируемой величины различают три типа систем: стабилизирующие, программные и следящие.
Стабилизирующие САР предназначены для поддержания регулируемых величин в определенных, наперёд заданных пределах (рис. 1.6). Большинство САР используются именно для целей стабилизации. В качестве примеров можно указать на системы поддержания частоты тока электростанции, температуры охлаждения двигателей, уровня воды и давления пара в котлах и многие другие. Для этих систем характерно постоянство заданного значения регулируемой величины.
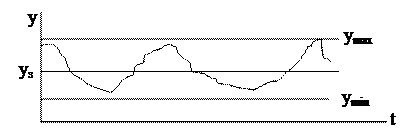 |
Рис. 1.6 Стабилизирующая САР.
Программные САР (системы программного регулирования) осуществляют изменение регулируемой величины во времени по определённой, наперёд заданной программе (рис.1.7). Эта программа хранится в памяти регулятора. Пример такой системы – система дистанционного автоматизированного управления (ДАУ), вводящая главный судовой двигатель в заданный режим работы. У этих систем заданное значение регулируемой величины изменяется во времени, и закон изменения (один или несколько – на выбор человека) заложен в регулятор.
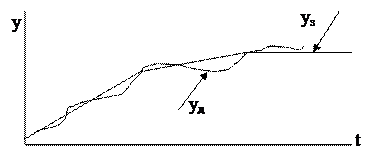 |
Рис.1.7 Система программного регулирования.
Следящие системы изменяют регулируемую величину в зависимости от изменения каких-либо внешних факторов, для которых закон изменения заранее не известен. Пример – система радиолокационного сопровождения (слежения) объекта, движущегося по неизвестной для наблюдателя траектории.
Независимо от типа рассмотренных систем всем им присуще общее свойство: действительное (фактическое) значение регулируемой величины должно быть с достаточной точностью близким к её заданному значению (в идеале – абсолютно точно равняться): у д =у з
По способу формирования и передачи сигнала различают автоматические системы управления непрерывные и дискретные. В непрерывных системах управляющие воздействия представляют собой непрерывные функции времени, в дискретных системах - в отдельные фиксированные моменты времени. Сигнал управления в последнем случае формируется по дискретным значениям выходной переменной и контролируемого возмущения. Эти значения могут соответствовать:
- произвольным значениям сигналов в фиксированные моменты времени (дискретизация по времени – рисунок 1.8, а);
- фиксированным значениям в произвольные моменты времени (дискретизация по уровню – рисунок 1.8, б);
- фиксированным значениям, ближайшим к произвольным значениям сигнала в фиксированные моменты времени (дискретизация по времени и по уровню – рисунок 1.8, в).
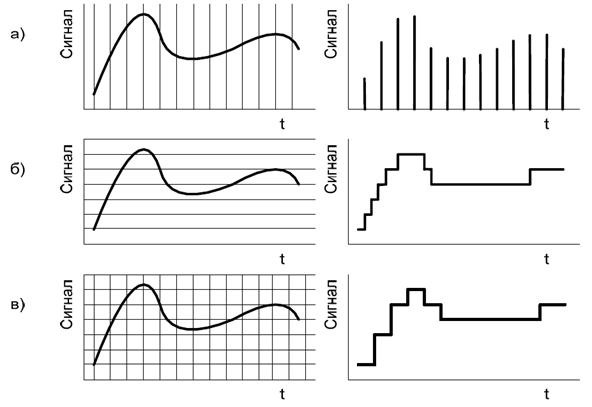
Рис. 1.8 Дискретизация сигнала
Если хотя бы одна переменная, характеризующая состояние системы квантована по времени, то она относится к импульснымавтоматическим системам. Если хотя бы одна переменная, характеризующая состояние системы квантована по уровню, то она относится к релейнымавтоматическим системам. Если хотя бы одна переменная, характеризующая состояние системы квантуется по времени и по уровню, то она относится к цифровымавтоматическим системам.
По числу входных и выходных переменных объекта управления различают системы одномерные (одна входная переменная, одна выходная переменная – рисунок 1.9, а), многомерные (несколько входных переменных, несколько выходных переменных – рисунок 1.9, б), множественные (несколько входных переменных, одна выходная переменная – рисунок 1.9, в) или одна входная переменная и несколько выходных переменных.
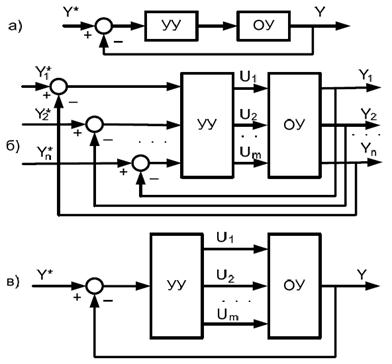
Рис. 1.9 Структуры систем управления
По возможности изменения структуры различают системы с постоянной и переменной структурой.
Среди систем с переменной структурой можно выделить системы с переменной структурой регулятора (рисунок 1.0, а) и системы с переменной структурой объекта управления (рисунок 1.0, б).
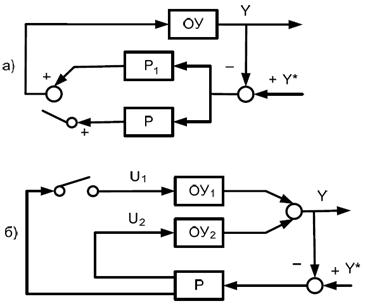
Рис. 1.10 Системы с переменной структурой
Различают также системы управления линейные и нелинейные. К линейным системам управления относятся системы для которых выполняется принцип суперпозиции – реакция системы управления на сумму воздействий равна сумме реакций системы на каждое воздействие. К нелинейным - системы включающие в себя хотя бы один нелинейный элемент – зубчатая передача, усилитель с насыщением, реле с зоной нечувствительности, компаратор и так далее.
Линейные системы описываются линейными дифференциальными уравнениями вида:
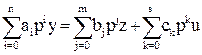 .
.
В таких системах функции и их производные входят линейно.
Нелинейные САР описываются нелинейными дифференциальными уравнениями, например,
p2y + (py)3 + y*py + F(y) = z.
В последнем уравнении подчёркнуты признаки нелинейности. Достаточно одного такого признака, чтобы система считалась нелинейной. Наиболее часто нелинейность обусловлена наличием нелинейных функций F(y), которые называются типовыми нелинейными характеристиками. В рамках курса «Теория автоматического управления» будут рассматриваться только линейные системы.
Основной математический аппарат – это дифференциальные уравнения для непрерывных систем и разностные уравнения для дискретных систем. Для первых в общем случае математическое описание, связывающее регулируемую величину с возмущающим и управляющим воздействиями, содержит указанные функции и их производные и имеет вид
F(y, y', y '', … y (n), z, z', z'', … z(m), u, u', u'', … u(s), t) = 0.
Во многих случаях применением корректных упрощений приходят к описанию системы в форме линейного дифференциального уравнения вида
n m s
å a i y (i) = å b j z (j) + å c k u (k),
i=0 j=0 k=0
в котором коэффициенты а, в, с могут быть либо функциями времени, либо постоянными величинами. Структура разностных уравнений аналогична.
 2014-02-02
2014-02-02 1649
1649








