Система автоматического регулирования и дистанционного измерения температуры в камере (рис. 2.15, а)
САР уровня воды в резервуаре (рис. 2.14, а)
САР температуры в камере (рис. 2.13, а)
САР уровня воды в резервуаре (рис. 2.12, а)
Система регулирования уровня жидкости в резервуаре (рис. 2.11, а)
Регулятор с гибкой обратной связью (рис.2.9)
Регулятор частоты вращения вала непрямого действия (рис 2.5)
Регулятор частоты вращения вала главного судового дизеля (рис. 2.3)
При, например, возрастании сопротивления вращению гребного винта частота вращения вала снижается. Грузики регулятора Г (чувствительный элемент) приводятся во вращение от вала двигателя. При снижении частоты вращения центробежная сила грузиков уменьшается, и под действием пружины П (задающее устройство) муфта регулятора М (сравнивающее устройство) перемещается вниз, вызывая через рычаг перемещение рейки топливных насосов Р (регулирующий орган) в сторону увеличения подачи топлива (+).
Регулятор прямого действия. Как и предыдущий, он на различных установившихся режимах поддерживает различные частоты вращения, поскольку различным нагрузкам двигателя должны соответствовать различные положения рейки топливных насосов, что по конструкции регулятора возможно при различных положениях муфты, а значит, при различных частотах вращения. Изменением затяжки пружины можно изменить задаваемую частоту вращения.
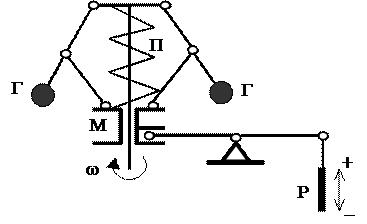 |
Рис.2.3 Центробежный регулятор частоты вращения вала прямого действия
Функциональная схема автоматизации (Рис. 2.4):
2.1 – первичный преобразователь частоты вращения SE;
2.2 – исполнительный механизм (рычаг);
3.3 – рейка ТНВД.
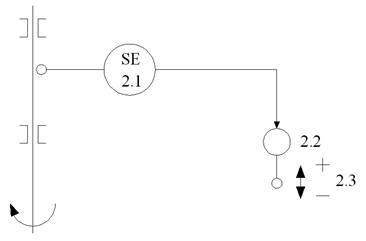
Рис. 2.4 Функциональная схема центробежного регулятора частоты вращения вала прямого действия
Здесь перемещение муфты приводит к перемещению золотника гидравлического усилителя, открывающего поступление силового масла (от насоса – дополнительного источника энергии) в одну из полостей поршневого сервомотора (исполнительный механизм) и сообщающего другую его полость со сливом. Сервомотор перемещает рейку топливных насосов в направлении соответствующего изменения топливоподачи.
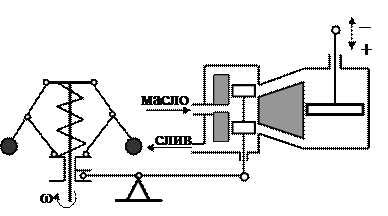
Рис. 2.5 Регулятор частоты вращения вала непрямого действия
Этот регулятор является астатическим, и объяснить такое его свойство можно путём следующих рассуждений. Установившийся режим наступает, когда прекращается движение рейки топливных насосов. Для этого золотник должен занять единственное положение, соответствующее полному перекрытию масляных каналов его поясками. По конструкции регулятора это возможно при единственном положении муфты, то есть при единственной частоте вращения. Рейка же топливных насосов займёт положение, соответствующее необходимой для конкретного режима топливоподаче.
Из сравнения рассмотренных регуляторов можно сделать заключение: если положение регулирующего органа однозначно связано с положением измерителя, то регулятор и система будут статическими. Если же эта связь не является однозначной, - регулятор и система астатические.
Последнему из рассмотренных регуляторов присущ серьёзный недостаток, заключающийся в возможности колебаний частоты вращения. Дело в том, что в начале переходного процесса происходит быстрое и сильное перемещение золотника и большое открытие им каналов сервомотора. Поршень при этом движется с высокой скоростью и может пройти дальше того положения, которое соответствует новому установившемуся режиму, это вызовет заброс частоты вращения, и регулятору придётся работать в обратном направлении. Достижение нового установившегося режима будет сопровождаться колебаниями регулируемой величины, что часто нежелательно.
С целью уменьшения склонности системы к колебаниям возникает идея: заставить поршень сервомотора замедлять своё движение, организовав воздействие самого поршня на золотник в направлении, противоположном смещению последнего под действием муфты. Это достигается введением в конструкцию регулятора корректирующего устройства - элемента дополнительной обратной связи.
Функциональная схема автоматизации (Рис. 2.6):
3.1 – первичный преобразователь частоты вращения SE;
3.2 – регулятор частоты вращения SC;
3.3 – исполнительный механизм (гидравлический сервомотор);
3.4 – рейка ТНВД.
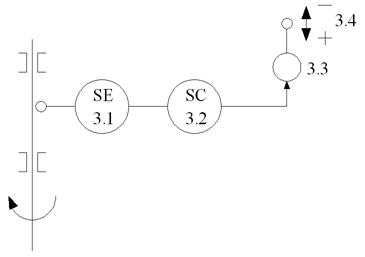
Рис. 2.6 Функциональная схема центробежного регулятора частоты вращения вала непрямого действия
2.4 Регулятор с жёсткой обратной связью (рис 2.7)
При, например, снижении частоты вращения муфта смещается вниз, и рычаг бав поворачивается относительно точки б, которая в этот момент является мгновенным центром вращения. Золотник, как и точка а, перемещается вниз, открывая доступ силового масла в нижнюю полость
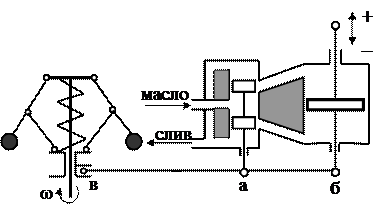 |
Рис.2.7 Регулятор с жёсткой обратной связью
сервомотора и сообщая его верхнюю полость со сливом. Поршень идёт вверх на увеличение топливоподачи.
Теперь рычаг бав поворачивается вокруг точки в (нынешнего мгновенного центра вращения), и золотник перемещается в направлении закрытия каналов, уменьшая скорость движения поршня и препятствуя тем самым колебаниям рейки топливных насосов. Таким образом, рычаг бав представляет собою корректирующее устройство типа жесткой обратной связи.
Однако получение такого качества работы регулятора достигается ценой снижения точности в установившихся режимах. В самом деле, учитывая условие установившегося режима (единственное положение золотника и точки а) для изменения топливоподачи необходимо изменение положения муфты, а значит, частоты вращения вала.
Стремление улучшить и это качество приводит к идее организации такой обратной связи, которая бы в начале переходного процесса работала аналогично только что рассмотренной, а в конце процесса регулирования исчезала бы. В автоматике такие связи называют гибкими, или исчезающими.
Функциональная схема автоматизации (Рис. 2.8):
4.1 – первичный преобразователь частоты вращения SE;
4.2 – регулятор частоты вращения SC;
4.3 – исполнительный механизм (гидравлический сервомотор);
4.4 – жёсткая обратная связь;
4.5 – рейка ТНВД.
В этой конструкции поршень сервомотора взаимодействует с рычагом обратной связи через цилиндр устройства, именуемого изодромом (в переводе с греческого "изодромный" означает "равнобежный"), представляющим собою комбинацию из пружины и цилиндра с поршнем. Цилиндр заполнен маслом и имеет канал для перетекания масла, снабжённый клапаном, проходное сечение которого можно изменять. Поршень изодрома жестко связан с поршнем сервомотора. Пружина изодрома в установившихся режимах полностью разгружена, поэтому точка б на установившихся режимах находится в единственном положении, в единственном же положении находится и золотник, а потому и муфта регулятора, что соответствует постоянной частоте вращения вала на всех установившихся режимах. Поршень сервомотора и рейка топливоподачи занимают соответствующее нужное положение.
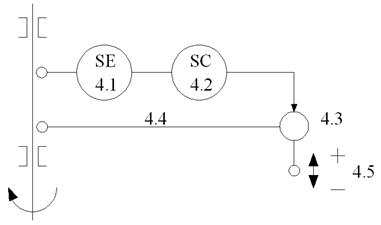
Рис. 2.8 Функциональная схема центробежного регулятора частоты вращения вала непрямого действия с жёсткой обратной связью
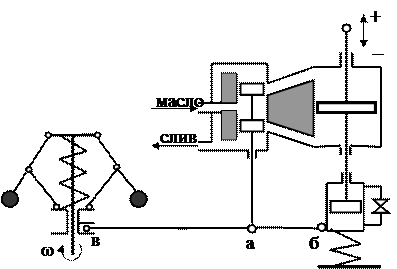 |
Рис. 2.9 Регулятор с гибкой обратной связью.
В переходных же процессах, особенно в их начале, при быстром движении поршня сервомотора он увлекает за собой цилиндр изодрома, поскольку масло не успевает перетекать между полостями вследствие малого проходного сечения клапана, и тем самым рычаг бав оказывает на золотник действие, описанное в предыдущем случае.
Функциональная схема автоматизации (Рис. 2.10):
5.1 – первичный преобразователь частоты вращения SE;
5.2 – регулятор частоты вращения SC;
5.3 – исполнительный механизм (гидравлический сервомотор);
5.4 – обратная связь, которая на установившихся режимах прекращает действовать;
5.5 – рейка ТНВД.
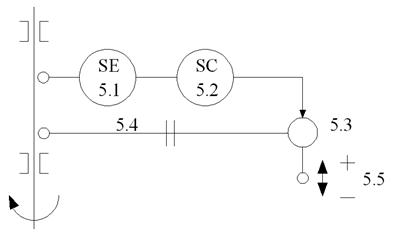
Рис. 2.10 Функциональная схема центробежного регулятора частоты вращения вала непрямого действия с гибкой обратной связью
Это есть пример системы автоматического регулирования по возмущению. Главное возмущение λ – это расход жидкости Q в из резервуара А. Если подача Q п равна расходу Q в, уровень жидкости Н не изменяется. Для измерения Q в используется труба Вентури 5 с дифференциальным манометром 4. Увеличение Q в приводит к увеличению разности р1 – р2, диафрагма дифференциального манометра перемещается вправо и тянет за собой напорную трубку 3. Вследствие этого давление в нижней части поршневого серводвигателя превышает давление в верхней части, поршень немного смещается вверх, и клапан 1 частично открывается, увеличивая подачу Q п. Если же равновесие нарушается вследствие уменьшения, благодаря работе регулятора подача Q п уменьшается.
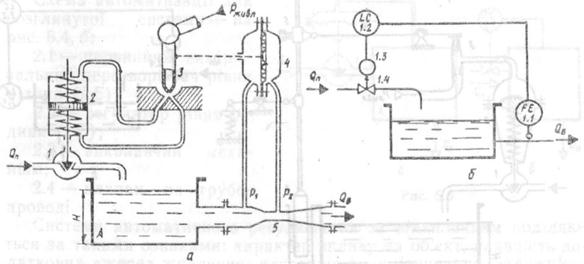
Рис. 2.11 Принципиальная и функциональная схемы САР уровня жидкости в резервуаре
Функциональная схема автоматизации для данной системы изображена на рисунке 2.11, б:
1.1 – первичный измерительный преобразователь расхода жидкости (FE);
1.2 – регулятор уровня жидкости (LC);
1.3 – исполнительный механизм, который после прекращения подачи распорядительного сигнала открывает регулирующий орган;
1.4 – клапан на трубопроводе.
Данная система осуществляет регулирование по принципу обратной связи. Если подача воды Q п равна расходу Q в, уровень Н не изменяется. Если же Q в уменьшается, уровень Н воды начинает увеличиваться, буйковый преобразователь 6 поднимается вверх, через рычаг 4 прикрывает сопло вторичного преобразователя сопло-заслонка 3, давление воздуха на его выходе увеличивается и мембранный серводвигатель 2 прикрывает клапан 1, уменьшая подачу Q п. При нарушении равновесия вследствие увеличения Q в регулятор обеспечивает соответствующее увеличение Q п. С помощью фиксатора 5 можно изменять значение уровня Н, который будет поддерживать регулятор: если фиксатор переместить вниз, регулятор будет поддерживать более низкий уровень воды, если же фиксатор переместить вверх – более высокий уровень. Говорят, что перемещение фиксатора даёт возможность менять уставку регулятора. Уставка (γ) даёт возможность задавать необходимое значение регулируемой величины, которое должен поддерживать регулятор.
Функциональная схема для данной системы изображена на рисунке 2.12, б:
2.1 – первичный измерительный преобразователь уровня жидкости (LE);
2.2 – регулятор уровня жидкости (LC);
2.3 – исполнительный механизм;
2.4 – клапан на трубопроводе.
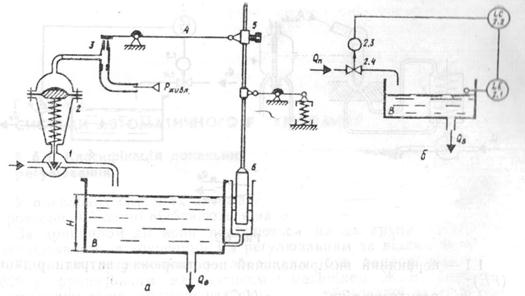
Рис. 2.12 Принципиальная и функциональная схемы САР уровня воды в резервуаре
Данная система является примером стабилизирующей системы. В данном случае регулятор поддерживает температуру в камере К на постоянном уровне, который задаётся уставкой (γ). В камере К нагревание осуществляется с помощью электронагревателя ЕК. Первичным измерительным преобразователем есть термопара, электродвижущая сила et которой сравнивается с напряжением Δ U, которое снимается с делителя R и играет роль уставки γ. Делитель R питается от источника стабильного напряжения U ст. Поскольку et и Δ U включены навстречу друг другу, при Δ U = et их сумма равна нулю. Если температура в камере К выше заданной, то et > Δ U, величина et – Δ U превращается в переменное напряжение (1 – преобразователь постоянного напряжения в переменное), усиливается (2 – усилитель) и включает сервоэлектродвигатель 3, который перемещает ползун автотрансформатора 4 вниз, уменьшая напряжение питания нагревателя. В результате температура в камере К не превышает заданной границы. Если температура в камере ниже заданной, сервоэлектродвигатель переместит ползун автотрансформатора вверх, увеличивая температуру.
Функциональная схема описанной САР изображена на рис. 2.13, б:
6.1 – первичный измерительный преобразователь температуры (ТЕ);
6.2 – регулятор температуры (ТС);
6.3 – исполнительный механизм, который после окончания подачи распорядительного сигнала оставляет регулирующий орган в неизменном состоянии;
6.4 – регулируемый орган (автотрансформатор).

Рис. 2.13 Принципиальная и функциональная схемы САР температуры в камере
Данную САР можно отнести к следящим системам. В такой системе автоматического регулирования выходной сигнал должен отображать входное регулирующее действие, которое изменяется по произвольному закону. Ползун С реостата R 1 перемещается в зависимости от изменения уровня воды в резервуаре. Если потенциал точки D отличается от потенциала точки C, разность потенциалов UC – UD превращается в переменное напряжение, усиливается и включает конденсаторный электродвигатель, который перемещает ползун D до тех пор, пока UD не сравняется с UC. Таким образом, ползун D следит за положением ползуна С и повторяет все его перемещения. Такая система может быть использована для измерения уровня воды в резервуаре.
Функциональная схема такой системы приведена на рис. 2.14, б:
8.1 – первичный измерительный преобразователь уровня жидкости (LE);
8.2 – дополнительный преобразователь сигнала уровня жидкости (LT);
8.3 – прибор, показывающий уровень жидкости в резервуаре (LI).
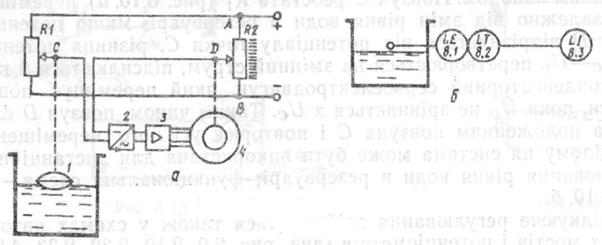
Рис. 2.14 Принципиальная и функциональная схемы САР уровня воды в резервуаре
На схеме: Q – камера, к которой поддерживается температура, r 1 – проводниковый терморезистор, r 2 – ползунковый реостат, r 3 и r 4 – резисторы, 1 – ползун реостата r 2, 2 – усилитель, PD – реверсивный конденсаторный сервоэлектродвигатель, 3 – счётно-регистрирующее устройство, SQ – контактное устройство (технологический контакт), КМ1, КМ2 и КМ3 – электромагнитные реле, EK – нагреватель камеры Q. Условием равновесия мостовой схемы является уравнение (r 1+ r 2 ') r 3 = r 2'' r 4); в этом случае UCD = 0 и ротор реверсивного сервоэлектродвигателя неподвижен. При изменении температуры изменяется и значение r 1, что вызывает появление UCD ≠ 0; это напряжение усиливается и приводит во вращение ротор сервоэлектродвигателя, одновременно изменяя r 2 ' и r 2'' (так быстрее будет достигнуто новое равновесие). Например, при увеличении контролируемой температуры увеличится, и для возобновления равновесия ползун 1 должен переместиться влево, одновременно уменьшая r 2 ' и увеличивая r 2''. Каждому значению температуры в камере Q будет соответствовать определённое положение ползуна при равновесии, а также положение показателя счётно-регистрирующего устройство.
Если температура в камере Q ниже установленного уровня, подвижный контакт SQ дотрагивается правого неподвижного, и срабатывает реле КМ1. Так как реле КМ2 отпущено, срабатывает и самоблокируется реле КМ3, включая нагреватель EK. Температура в камере увеличивается; когда ползун 1 переместит подвижный контакт влево, сработает реле КМ2, что разорвёт цепь катушки реле КМ3, которое выключит нагреватель EK. Температура начнёт понижаться, пока ползун 1 не отпустит подвижный контакт SQ, который при этом снова дотронется правого неподвижного и сработает реле КМ1. Принцип регулирования – по отклонению, характер воздействия – релейное, двухпозиционное; регулятор – стабилизирующий.
Функциональная схема автоматизации изображена на рис. 2.15, б:
11.1 – первичный измерительный преобразователь температуры (TE);
11.2 – вторичный преобразователь, предназначенный для дистанционной передачи измеряемой информации (ТТ);
11.3 – прибор измерительный (показания и регистрация) и регулирующий (TIRC);
11.4 – исполнительный механизм;
11.5 – регулируемый орган (контактное устройство).
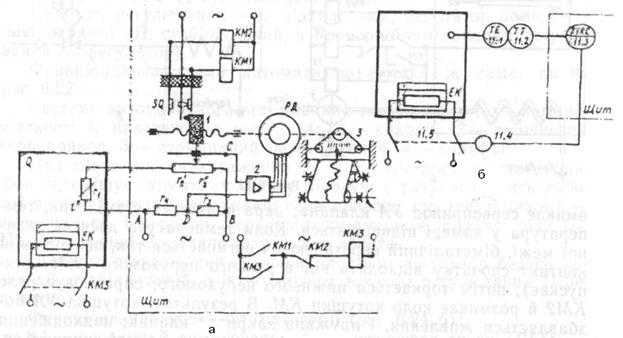
Рис. 2.15 Принципиальная и функциональная схемы САР и дистанционного измерения температуры в камере
Звено называют элементарным, если оно не может быть представлено как комбинация двух или более звеньев. Независимо от физической природы протекающих процессов всё многообразие элементарных звеньев по математическому описанию сводится к шести типам. Ниже они будут рассмотрены, и показаны графики переходных процессов в этих звеньях при скачкообразном сигнале на входе.
1.Безинерционное звено:
| y = kx | (3.1) |
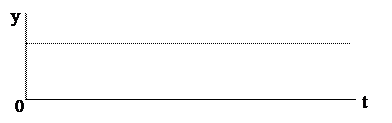 Свойства этого звена таковы, что оно мгновенно, без какого-либо запаздывания передаёт входной сигнал на выход (рис.3.1).Иногда поэтому его называют идеальным по быстродействию.
Свойства этого звена таковы, что оно мгновенно, без какого-либо запаздывания передаёт входной сигнал на выход (рис.3.1).Иногда поэтому его называют идеальным по быстродействию.
Рис. 3.1 Безинерционное звено.
Поскольку любое из реально существующих звеньев обладает большей или меньшей инерционностью, такое представление о динамических свойствах звена является определенной идеализацией, допустимой лишь при сравнении двух инерционных звеньев по продолжительности переходных процессов в них. По современному состоянию техники одно звено можно считать безинерционным по сравнению с другим, если постоянная времени первого хотя бы в 50 раз меньше, чем постоянная времени второго. Так, часто в процессах вывода на заданный режим главный судовой двигатель можно считать безинерционным по сравнению с судном.
2.Апериодическое звено первого порядка описывается уравнением вида:
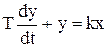 | (3.2) |
Для нахождения закона изменения регулируемой величины у во времени необходимо решить данное дифференциальное уравнение. Мы имеем дело с линейным неоднородным дифференциальным уравнением первого порядка. Для всех систем, описывающихся линейными дифференциальными уравнениями, справедлив принцип суперпозиции, согласно которому общий эффект от действия на систему суммы нескольких факторов равен сумме эффектов, вызываемых каждым отдельным фактором. Применительно к нашему объекту это означает, что можно рассмотреть изменение регулируемой величины под влиянием каждого из возмущений раздельно, а затем полученные результаты алгебраически сложить.
Решение данного уравнения ищется в виде
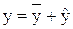 , , | (3.3) |
где 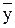 – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения
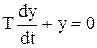 , , | (3.4) |
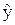 - частное решение уравнения (3.2).
- частное решение уравнения (3.2).
В качестве частного решения обычно интересуются новым установившимся значением регулируемой величины, то есть тем, которое она примет по окончании переходного процесса, вызванного воздействием в данном случае x. Примем, что закон изменения x – скачкообразный:
t < 0, x = 0, t ³ 0, x = x 0 =const.
В нашем случае это соответствует мгновенному изменению относительного положения рейки топливоподачи на величину x0. Таким образом, условия нового установившегося режима выглядят так:
x = x0; 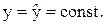 | (3.5) |
Подставив эти условия в уравнение (3.2), получим
 y = kx 0.
y = kx 0.
Общее решение однородного уравнения ищется в форме
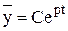 ,
,
где C – постоянная интегрирования, p – корень характеристического уравнения
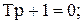
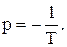
Таким образом,
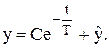 | (3.6) |
Постоянная интегрирования определяется на основании начальных условий. Обычно в качестве таковых задаются условиями исходного установившегося режима, когда ещё не было изменения регулируемой величины, и они выглядят так:
t = 0, y=0.
Подставив начальные условия в уравнение (3.6), получим
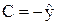 ,
,
и окончательно
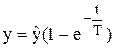 | (3.7) |
График переходного процесса.
На рис. 3.2 представлена графически зависимость регулируемой величины у во времени, называемая графиком переходного процесса. Здесь ЛНУР – линия нового установившегося режима. Очевидно, что она является асимптотой для кривой - графика переходного процесса. Эта кривая (в математике она имеет специальное название – экспонента) обладает следующим свойством: отрезок, отсекаемый на ЛНУР касательной к экспоненте в какой-либо точке и перпендикуляром из этой точки, численно равен постоянной времени. Тогда можно дать толкование физическому смыслу постоянной времени, если рассмотреть такое построение из начала координат.
Постоянная времени – это время, за которое регулируемая величина достигла бы значения, соответствующего новому установившемуся режиму, если бы она изменялась с постоянной скоростью, равной начальной скорости её изменения.
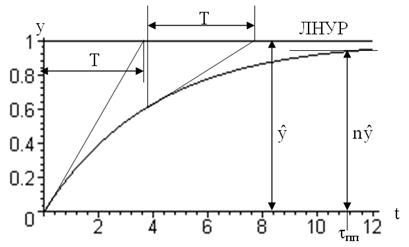
Рис.3.2. График переходного процесса в объекте регулирования
и постоянная времени.
Продолжительность переходного процесса в объекте регулирования
Теоретически для любого объекта выход регулируемой величины на новое установившееся значение продолжается бесконечно долго. На практике же можно встретить объекты, в которых переходный процесс происходит быстрее или медленнее. В автоматике широко применяется инженерное понятие продолжительности переходного процесса. Это такое время tпп, за которое регулируемая величина становится достаточно близкой к своему установившемуся значению (рис.3.2):
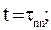 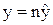 . . | (3.8) |
Здесь величина n близка к единице и характеризует точность приближения к установившемуся режиму.
Подставив (3.8) в (3.7) и выполнив упрощение, получим
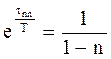 .
.
После логарифмирования обнаруживается связь между временем переходного процесса и постоянной времени:
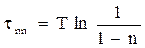 | (3.9) |
Часто считают переходный процесс практически окончившимся, когда регулируемая величина достигает 95% от нового установившегося значения, то есть принимают n = 0, 95. При этом оказывается, что
tпп @ 3Т.
Приведём практически встречающиеся значения постоянных времени судовых объектов регулирования, которые в первом приближении могут быть описаны дифференциальным уравнением первого порядка.
Судовые главные дизели – около 1 секунды.
Газотурбонагнетатели – несколько секунд.
Дизельгенераторы – 3…4 секунды.
Судовые паровые котлы – 10…15 минут.
Судно относительно изменения его скорости – 1…5 минут.
Различные теплообменные аппараты – минуты.
Электродвигатели – около 1 секунды.
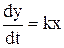 . . | (3.10) |
Прямое интегрирование при нулевых начальных условиях дает
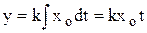 .
.
График переходного процесса приведен на рис. 3.3. Примерами таких звеньев являются различные счётчики, многие исполнительные механизмы.
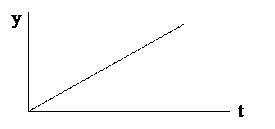 |
Рис. 3.3 Интегрирующее звено
4.Дифференцируюшее звено:
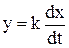 . . | (3.11) |
Это тоже в некотором роде идеализация. При скачкообразном сигнале на входе в моменты времени, не равные нулю, сигнал на выходе равен нулю, а в нулевой момент времени выходной сигнал имеет вид импульса, бесконечно большого по величине и бесконечно малого по продолжительности (рис. 3.4)
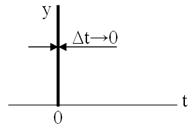
Рис. 3.4 Идеальное дифференцирующее звено.
5.Звено с «чистым», или транспортным запаздыванием. В таком звене выходная величина повторяет входную с отставанием на время «чистого» запаздывания t3 (рис. 3.5):
| y(t+t3) = x(t). | (3.12) |
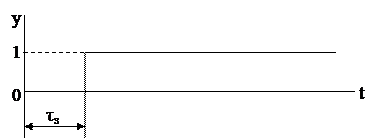
Рис. 3.5 Звено с «чистым» запаздыванием.
6. Звено второго порядка описывается уравнением вида:
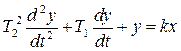 . . | (3.13) |
Коэффициент k называется коэффициентом усиления, а коэффициенты Т22 и Т1 имеют размерности соответственно квадрата и первой степени времени. Такое обозначение логично и удобно.
В результате решения данного диф. уравнения мы получим закон изменения во времени выходной величины у. Примем, как это уже стало привычным, что входная величина изменяется скачкообразно:
t < 0, х = 0; t ³ 0, х = х0 = const.
Решение уравнения (3.13) ищется в форме
у = 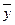 +
+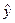 ,
,
где 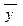 – общее решение соответствующего однородного уравнения
– общее решение соответствующего однородного уравнения
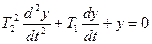 , , | (3.14) |
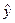 – частное решение уравнения (3.13).
– частное решение уравнения (3.13).
По аналогии с уравнением первого порядка частное решение как новое установившееся значение выходной величины будет
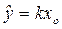 .
.
Общее решение уравнения (3.28) ищется в форме

 ,
,
где C1 и C2 – постоянные интегрирования, p1 и p2 – корни характеристического уравнения
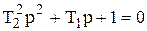 | (3.15) |
Таким образом,
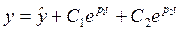 . . | (3.16) |
Постоянные интегрирования, определим на основании начальных условий. Исходный установившийся режим характеризуется следующими условиями:
t=0; у=0; 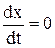 . . | (3.17) |
Подстановка (3.17) в (3.16) даёт
 | (3.18) |
Отсюда постоянные интегрирования
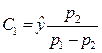 ; ; 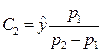 , , | (3.19) |
и окончательно
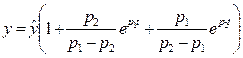 . . | (3.20) |
В зависимости от вида корней характеристического уравнения (вещественные, комплексные либо чисто мнимые) имеется три частных случая. Обратим, однако, внимание на то, что решение уравнения (3.13) в форме (3.20) получено для общего случая, независимо от вида корней.
6.А В случае, когда выполняется условие
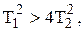
характеристическое уравнение имеет два вещественных отрицательных корня
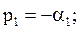
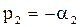 ,
,
и переходный процесс описывается формулой
 . . | (3.21) |
Соответствующий график переходного процесса показан на рис.3.6. Звено в этом случае называется апериодическим звеном второго порядка, чем подчёркивается факт отсутствия колебаний в переходном процессе.
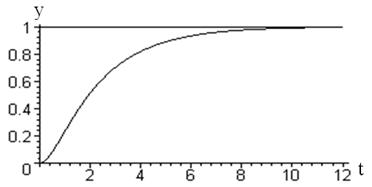
Рис. 3.6 Переходный процесс апериодического звена 2 порядка
6.Б В случае, когда
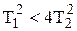 ,
,
корни характеристического уравнения комлексно-сопряжённые с отрицательной вещественной частью:
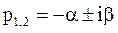 .
.
Подстановка этих значений в выражение (3.21) с учётом того, что, согласно формуле Эйлера,
e ±ibt =cosbt ± isinbt,
после простых преобразований приводит к такому результату:
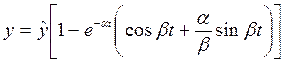 . . | (3.22) |
График переходного процесса для этого случая показан на рис. 3.7. Звено называется колебательным, и период колебаний выражается через частоту свободных колебаний так:
| Tкол=2p/b. | (3.23) |
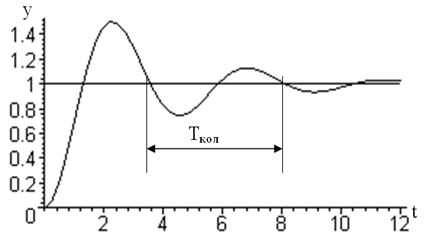
Рис. 3.7 Переходный процесс колебательного звена
 2014-02-02
2014-02-02 2604
2604








