В реальных условиях эксплуатации САР нередко подвергается действию периодических возмущающих сил, что сопровождается периодическими изменениями регулируемых величин и регулирующих воздействий. Таковы, например, колебания судна при ходе на волнении, колебания частоты вращения гребного винта и других величин. В ряде случаев амплитуды колебаний выходных величин системы могут достигать недопустимо больших значений, и это соответствует явлению резонанса. Последствия резонанса часто губительны для испытывающей его системы, например, опрокидывание судна, разрушение двигателя. В системах регулирования такие явления возможны при изменении свойств элементов, вызванном износами, заменой, перенастройкой, отказами. Тогда возникает необходимость либо определения безопасных диапазонов эксплуатационных условий, либо надлежащей настройки САР. Здесь будут рассмотрены эти вопросы в приложении к линейным системам.
Пусть некоторая система имеет нижепоказанную структуру:
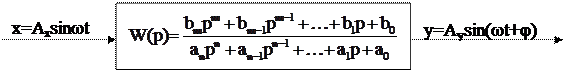 |
|
|
|
Рис. 5.1 САР в режиме вынужденных колебаний
Если на систему действует периодическое воздействие х с амплитудой Ах и круговой частотой w, то после окончания переходного процесса на выходе установятся колебания той же частоты с амплитудой Ау и смещенные относительно входных колебаний на фазовый угол j. Параметры выходных колебаний (амплитуда и фазовый сдвиг) зависят от частоты вынуждающей силы. Задача заключается в определении параметров выходных колебаний по известным параметрам колебаний на входе.
В соответствии с передаточной функцией САР, показанной на рис. 5.1, дифференциальное уравнение её имеет вид
| (anpn+an-1pn-1+…+a1p+a0)y=(bmpm+bm-1pm-1+…+b1p+b0)x. | (5.1) |
Подставим в (5.1) выражения для х и у, приведенные на рис. 5.1:
(anpn+an-1pn-1+…+a1p+a0)Aysin(wt+j)=
=(bmpm+bm-1pm-1+…+b1p+b0)Axsinwt. (5.2)
Если рассматривать картину колебаний, смещенную на четверть периода, то в уравнении (5.2) функции синусов сменятся функциями косинусов:
(anpn+an-1pn-1+…+a1p+a0)Aycos(wt+j)=
=(bmpm+bm-1pm-1+…+b1p+b0)Axcoswt. (5.3)
Умножим уравнение (5.2) на i =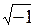 и сложим полученное с (5.3):
и сложим полученное с (5.3):
 (anpn+an-1pn-1+…+a1p+a0)Ay[cos(wt+j)+isin(wt+j)]=
(anpn+an-1pn-1+…+a1p+a0)Ay[cos(wt+j)+isin(wt+j)]=
= (bmpm+bm-1pm-1+…+b1p+b0)Ax(coswt+isinwt). (5.4)
Применяя формулу Эйлера
exp(±ibt)=cosbt ± isinbt,
приведём уравнение (5.4) к виду
(anpn+an-1pn-1+…+a1p+a0)Ayexp[i(wt+j)]=
= (bmpm+bm-1pm-1+…+b1p+b0)Axexp(iwt). (5.5)
Выполним операцию дифференцирования по времени, предусмотренную оператором р=d/dt:
[an(iw)n+an-1(iw)n-1+…+a1iw+a0]Ayexp[i(wt+j)]=
=[bm( iw)m+bm-1( iw)m-1+…+b1iw+b0]Axexp(iwt). (5.6)
После простых преобразований, связанных с сокращением на exp(iwt), получаем
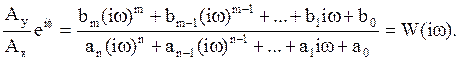 (5.7)
(5.7)
Правая часть выражения (5.7) похожа на выражение передаточной функции САР и может быть получена из него заменой p=iw. По аналогии она называется комплексной передаточной функцией W(iw), или амплитудно - фазовой характеристикой (АФХ). Нередко употребляют также термин частотная характеристика. Понятно, что эта дробь является функцией комплексного аргумента и может быть представлена ещё и в таком виде:
|
|
|
| W(iw) = M(w) +iN(w), | (5.8) |
где M(w) и N(w) – соответственно вещественная и мнимая частотные характеристики.
Отношение Ау/Ах есть модуль АФХ и является функцией частоты:
Ау/Ах=R(w)
и называется амплитудно- частотной характеристикой (АЧХ). Фазовый сдвиг
j =j (w) - также функция частоты и называется фазовой частотной характеристикой (ФЧХ). Вычисляя R(w) и j(w) для диапазона частот (0…¥), можно построить на комплексной плоскости в координатах M(w) и iN(w) график АФХ (рис. 5.2).
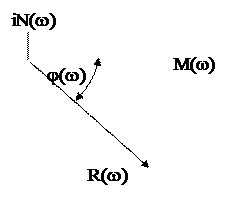
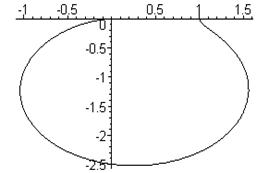
Рис. 5.2 График АФХ
Очевидны следующие соотношения:
M = Rcosj; N = Rsinj;
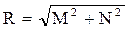 ; j = arctg(N/M). ; j = arctg(N/M). | (5.9) |
Амплитудно-частотная характеристика.
АЧХ любой системы представляет наибольший интерес, поскольку даёт возможность определить амплитуду колебаний выходной величины при известных амплитуде и частоте входной величины. На рис. 5.3 показаны возможные на практике виды АЧХ.
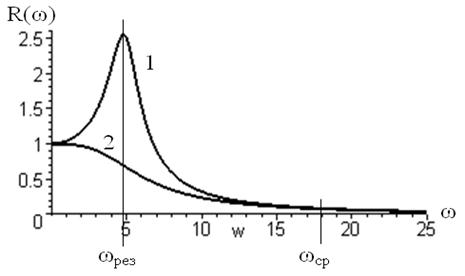
Рис. 5.3 Амплитудно-частотные характеристики
На АЧХ системы 1 виден резонансный пик, соответствующий наибольшей амплитуде вынужденных колебаний. Работа в зоне около резонансной частоты может оказаться губительной и часто вообще недопустима правилами эксплуатации конкретного объекта регулирования. АЧХ вида 2 не имеет резонансного пика и для механических систем более предпочтительна. Видно также, что с увеличением частоты амплитуда выходных колебаний уменьшается. Физически это легко объясняется: любая система в силу присущих ей инерционных свойств легче подчиняется раскачиванию низкими частотами, чем высокими. Начиная с некоторой частоты, колебания на выходе становятся незначительными, и эту частоту называют частотой среза, а диапазон частот ниже частоты среза называют полосой пропускания частот. В теории автоматического регулирования за частоту среза принимают такую, при которой значение АЧХ в 10 раз меньше, чем при нулевой частоте. Свойство системы гасить высокочастотные колебания называется свойством фильтра низких частот.
Рассмотрим методику расчета АЧХ на примере звена второго порядка, дифференциальное уравнение которого
| (T22p2 + T1p + 1)y = kx. | (5.10) |
В задачах вынужденных колебаний часто используют более наглядную форму уравнения
| (p2 +2xw0p + w02)y = kw02x, | (5.11) |
где 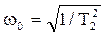 называется собственной частотой колебаний при отсутствии затухания, x =T1w0/2 - коэффициент затухания.
называется собственной частотой колебаний при отсутствии затухания, x =T1w0/2 - коэффициент затухания.
Передаточная функция при этом выглядит так:
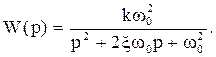 | (5.12) |
Заменой p = iw получаем амплитудно-фазовую характеристику
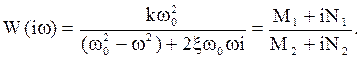 | (5.13) |
Используя правило деления комплексных чисел, получаем выражение для АЧХ:
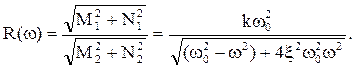 | (5.14) |
Определим резонансную частоту, при которой АЧХ имеет максимум. Это соответствует минимуму знаменателя выражения (3.66). Приравнивая нулю производную знаменателя по частоте w, имеем:
| 2(w02 - w2)(-2w) +4x2w02*2w = 0, | (5.15) |
откуда получаем значение резонансной частоты, не равное нулю:
 wрез = w0Ö 1 - 2x2. wрез = w0Ö 1 - 2x2. | (5.16) |
Проанализируем это выражение, для чего рассмотрим отдельные случаи, которым соответствуют различные значения коэффициента затухания.
1. x = 0. Резонансная частота равна собственной, и модуль АЧХ при этом обращается в бесконечность. Это случай так называемого математического резонанса.
2. 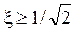 . Поскольку частота выражается положительным числом, а из (5.16) для этого случая получается либо нуль, либо мнимое число, следует вывод, что при таких значениях коэффициента затухания АЧХ не имеет резонансного пика (кривая 2 на рис. 5.3).
. Поскольку частота выражается положительным числом, а из (5.16) для этого случая получается либо нуль, либо мнимое число, следует вывод, что при таких значениях коэффициента затухания АЧХ не имеет резонансного пика (кривая 2 на рис. 5.3).
3.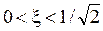 . АЧХ имеет резонансный пик, причём с уменьшением коэффициента затухания резонансная частота приближается к собственной и резонансный пик становится выше и острее.
. АЧХ имеет резонансный пик, причём с уменьшением коэффициента затухания резонансная частота приближается к собственной и резонансный пик становится выше и острее.
 2014-02-02
2014-02-02 3652
3652
