Пример
Задана исходная система:
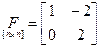 ;
; 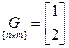 ;
;
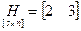 ;
;
Решение:
- Строим матрицу управления
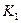
Это одномерная система, т.к. величины скалярные.
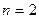 ,
, 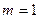 ,
, 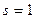 .
.
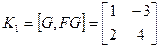 ;
;
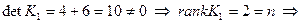 система управляема.
система управляема.
- Найдем характеристические числа матрицы динамики исходной системы
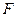 :
:
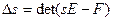 ;
;
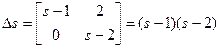 ;
;
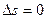 ;
;
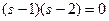 ;
;
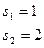 ;
;
 ;
;
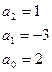 ; – система устойчива.
; – система устойчива.
Пусть запас устойчивости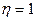 .
.
- Зададим
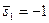 и
и 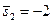
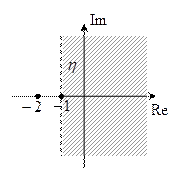
Находим коэффициенты характеристического уравнения желаемой системы:
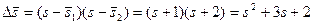 ;
;
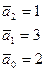
- Вычисляем матрицу

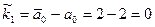 ;
;
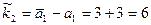 ;
;
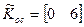 .
.
- Вычисляем матрицу перехода к новому базису
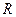 :
:
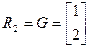 ;
;
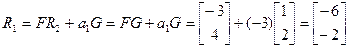 ;
;
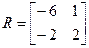 .
.
- Вычислим матрицу
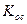 в старом базисе:
в старом базисе:
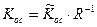 ;
;
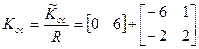 ;
;
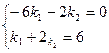 ;
;
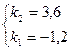 ;
;
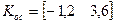 .
.
- Построим регулятор
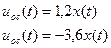 ;
;
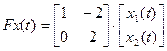 ;
; 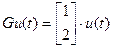 ;
;
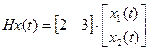 ;
;
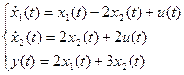 ;
;
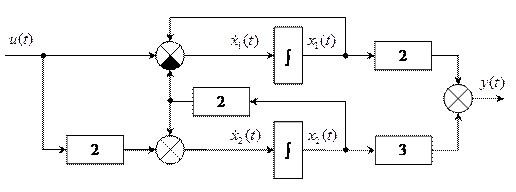
Линейную систему с помощью ООС по состоянию 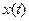 можно перевести в состояние покоя
можно перевести в состояние покоя 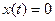 , причем этому движению можно придать любые динамические свойства. Эту возможность можно реализовать, имея полную информацию о состоянии системы, но в реальности часто нет возможности прямого измерения всего вектора состояния.
, причем этому движению можно придать любые динамические свойства. Эту возможность можно реализовать, имея полную информацию о состоянии системы, но в реальности часто нет возможности прямого измерения всего вектора состояния.
Если нельзя измерить, то оказывается можно построить динамическую линейную систему – наблюдатель, выходные переменные которой асимптотически приближаются к координатам состояния управляемой системы.

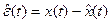 ; – ошибка оценки (значений) вектора состояний
; – ошибка оценки (значений) вектора состояний
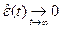 ;
;
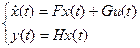 .
.
 2014-02-02
2014-02-02 465
465







