Оптимальное управление САУ

Пример

Алгоритм построения регулятора и наблюдателя

; .

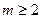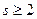1. Преобразовать матрицу 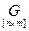в столбец 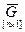путем замены
   ;
   при умножении на которую справедливо, что пара матриц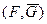 не вырождена.

1. (последний шаг)
   ;
   

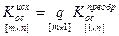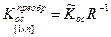
Дана система производства и управления запасами, в которой объем выпускаемой продукции 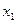, а объем запасов .

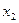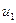– интенсивность производства;

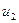– объем поставок производства.

Рассматривается непрерывный характер производства, которому соответствует следующая модель:

;

;

; .

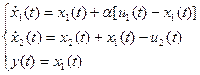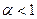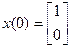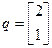Необходимо:

1. Оценить устойчивость системы;
2. Построить переходный процесс обусловленный ненулевыми начальными условиями;
3. Построить стабилизирующую отрицательную обратную связь.

Решение:

;

;

; ;

.

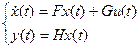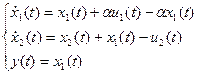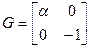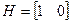1. Преобразуем матрицу 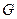в столбец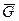
   ;
   
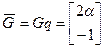   Определим управляемость системы:
   ;
   .

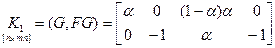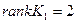1. Определим характеристические числа
   ;
   ;
   ;
   .
   
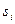
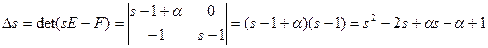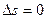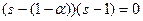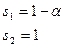   Найдем коэффициенты характеристического уравнения:
   ;
   

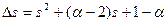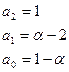
1. Пусть
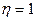
   Зададим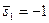 и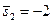
   Находим коэффициенты характеристического уравнения желаемой системы
   ;
   

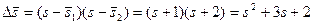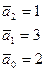
1. Вычисляем матрицу
   ;
   ;
   .

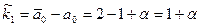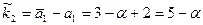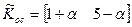1. Вычисляем матрицу перехода к новому базису
   ;
   

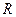
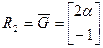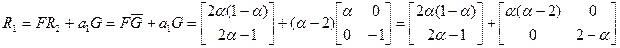
Невозможно слагать матрицы разных размерностей.

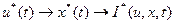
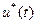– наилучшая управляемость системы

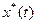– оптимальная траектория движения системы

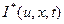– функционал (оптимальное значение)

В задачах детерминированного синтеза выделяют задачу построения оптимальных траекторий УУ 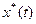, т.е. определение оптимального управления .

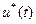Задача оптимизации заключается в том, как что-либо делать наилучшим образом. В ТУ «что-либо делать» означает управлять динамической системой.

При выборе управления не существует абсолютной оптимизации, поэтому при выборе наилучшего управления необходимо определить понятие оптимизации. Для этого с каждой задачей управления, стабилизации, идентификации связывают некоторое число, которое называют показателем качества. Значение этого показателя качества есть мера того, на сколько должно управление обеспечивать функционирование системы по отношению к выбранным критериям. Показатель качества – это математическая модель требований качества, средство оценки желаемого характера поведения системы.

Экстремальное значение показателя качества – это критерий качества функционирования, обозначим 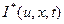(критерий, который определяет доход или стоимость для любого предложенного закона управления называют функцией стоимости или целевой функцией).

В задачах оптимального управления задают две проблемы:

1. Выбор математической модели, в состав которой входит выбор функционала, который зависит от выбора управляющего показателя качества воздействия, состояния системы 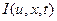. Определить состав ограничений, в пределах выполнения которых может быть реализована траектория движения системы (и в первую очередь это ограничение связано с обеспечением траектории движения системы).
2. Выбор математического метода для решения задачи оптимального управления. В общем случае решения поставленной задачи не существует. Так как задача является вариационной, то решение даже вариационными методами трудное, а иногда даже не возможное. Поэтому были разработаны новые методы для задач оптимального управления САУ, к ним относятся:
   методы Калмана;
   принцип максимума Понтрягина;
   методы динамического программирования Беллмана.