Пример
Предприятие изготавливает два вида красок:
- для наружных работ (краска 1-го вида)
- для внутренних работ (краска 2-го вида)
Продукция обоих видов поступает в продажу.
Для производства обоих видов красок используется два исходных продукта A и B.
Максимально возможные суточные запасы этих продуктов 6 и 8 тонн соответственно.
Расходы A и B на одну тонну соответствующих красок даны в таблице.
| Исходный продукт | Расход исходного продукта в тоннах на 1 тонну продукта | Максимально возможный запас | |
| краска 1-го вида | краска 2-го вида | ||
| A | |||
| B | |||
| опт. цена | 3 тыс. $ | 2 тыс. $ |
Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида не превышает суточный спрос на краску 1-го вида более чем на 1 тонну.
Кроме того, установлено, что спрос на краску 2-го вида не превышает 2 тонны в сутки.
Оптовые цены за 1 тонну равны.
Какое количество краски каждого вида должно производить предприятие чтобы получить максимальный доход от реализации.
Составить математическую модель.
Дано:
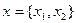 ,
, 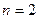 ; - количество произведенной продукции (краски) (в тоннах)
; - количество произведенной продукции (краски) (в тоннах)
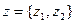 ,
, 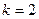 ; - спрос (в тоннах)
; - спрос (в тоннах)
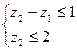 ;
;
Решение:

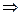
 ;
;
 ;
;
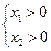 .
.
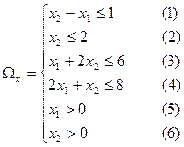 .
.
 .
.
Из всех программ 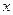 принадлежащих множеству
принадлежащих множеству  надо выбрать такую, которая бы соответствовала
надо выбрать такую, которая бы соответствовала 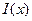 .
.
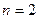 ;
;
 ; - число ограничений
; - число ограничений
Ограничения и 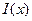 линейные, значит можно применить метод линейного программирования.
линейные, значит можно применить метод линейного программирования.
Графический метод линейного программирования. (Он может быть использован, если 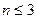 ).
).

Пространство  содержит бесконечное число допустимых решений соответствующих точкам многоугольника
содержит бесконечное число допустимых решений соответствующих точкам многоугольника 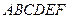 , а нам надо найти оптимальное решение, для этого необходимо определить в каком направлении возрастает целевая функция
, а нам надо найти оптимальное решение, для этого необходимо определить в каком направлении возрастает целевая функция  .
.
При графическом решении надо нанести ряд параллельных прямых соответствующих целевой функции при нескольких произвольных возрастающих значениях  , что позволит определить наклон целевой функции и направление в котором происходит ее увеличение.
, что позволит определить наклон целевой функции и направление в котором происходит ее увеличение.
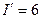 ;
; 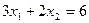 ;
;
 ;
; 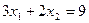 .
.
Найдем координаты точки  :
:
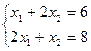 ;
;
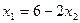 ;
;
 ;
; 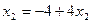 ;
;
 ;
;
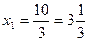 ;
;
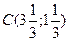 ;
;
 .
.
Определить  и найти оптимальное решение
и найти оптимальное решение  , считая что каждое из указанных ниже условий заменяет, а не дополняет соответствующие исходные данные, причем все остальные заданные соотношения остаются неизменными.
, считая что каждое из указанных ниже условий заменяет, а не дополняет соответствующие исходные данные, причем все остальные заданные соотношения остаются неизменными.
- максимальный спрос на краску 2-го вида равен 3 тонны в сутки;
- спрос на краску 2-го вида не менее 2 тонн в сутки;
- спрос на краску 2-го вида ровно на 1 тонну превышает спрос краски 1-го типа;
- допустимый суточный расход исходного продукта
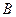 не меньше 8 тонн в сутки;
не меньше 8 тонн в сутки; - допустимый суточный расход исходного продукта
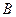 не меньше 8 тонн, а спрос на краску 2-го вида превышает спрос на краску 1-го вида не менее чем на 1 тонну.
не меньше 8 тонн, а спрос на краску 2-го вида превышает спрос на краску 1-го вида не менее чем на 1 тонну. - найти оптимальное решение при следующих значениях целевой функции:
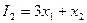 ;
; - найти оптимальное решение при следующих значениях целевой функции:
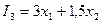 .
.
Решение:
 .
.
 .
.

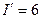 ;
; 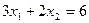 ;
;
 ;
; 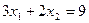 .
.
Найдем координаты точки  :
:
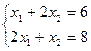 ;
;
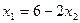 ;
;
 ;
; 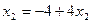 ;
;
 ;
;
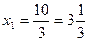 ;
;
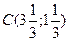 ;
;
 .
.
 2014-02-02
2014-02-02 412
412








