Пример
Дана система в виде:
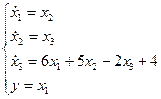
Построит регулятор системы такой, что после замыкания обратной отрицательной связью система должна иметь следующие корни характеристического уравнения:
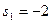 ,
, 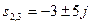 ;
;
запас устойчивости 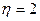 .
.
Решение:
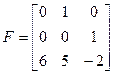 ;
; 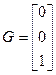 ;
; 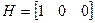 ;
; 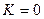 ;
;
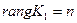 ;
;
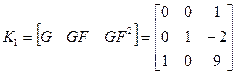 ;
; 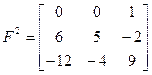 ;
;
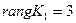 .
.
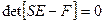 ;
;
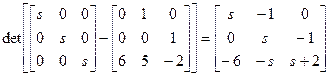 ;
;
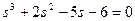 ;
;
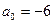 ;
; 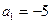 ;
; 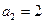 ;
; 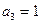 ;
;
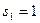 ;
; 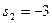 ;
; 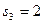
Характеристический многочлен (метод Гурвица)
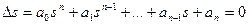 ;
;
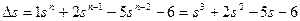 ;
;
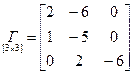 ;
;
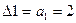 ;
;
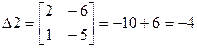 ;
;
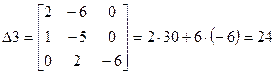 ;
;
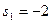 ;
; 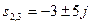 ;
;
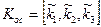
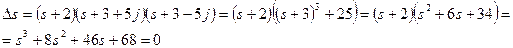 ;
;
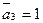 ;
; 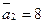 ;
; 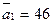 ;
; 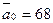 ;
;
При условии если матрица динамики находится в форме Калмана, тогда
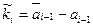 ;
;
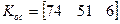 ;
;
- Если исходная система находится в форме Калмана, то матрица имеет вид
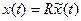 ;
;
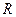 – единичная матрица, если в форме Калмана
– единичная матрица, если в форме Калмана
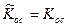 ;
;
 .
.
Исследование операций – комплекс научных методов, предназначенных для анализа и обоснования решений во всех областях целенаправленной деятельности человека
(широко используется для разработки ERP-систем Enterprise Research Planning).
Операция – это любое мероприятие или система действий объединенная единым замыслом и направленной к достижению единой цели.
Операция должна быть управляемой, т.е. должны существовать возможности воздействия на операции с целью выбора лучшего способа ее осуществления.
Решением называется всякий определенный способ осуществления операции.
Оптимальным решением называются те решения, которые по тем или иным соображениям предпочтительнее других.
Качество или эффективность операции – это свойство характеризующее степень приспособленности операции к выполнению поставленной задачи (требования).
Показатель качества операции – количественная мера качества операции.
Основные этапы исследования операции:
- Постановка задачи;
- Построение модели операции;
- Поиск решения;
- Корректировка модели;
- Реализация.
Модели операции
Модель – приближенное описание операции (один и тот же объект может иметь много различных моделей).
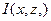 ;
;
 ; - вектор управляемых переменных
; - вектор управляемых переменных
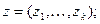 - вектор неуправляемых переменных
- вектор неуправляемых переменных
Требования к модели:
- Модель должна обеспечивать достаточную точность оценки критериев во всей области возможных решений
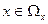 ; (омега – область допустимых значений)
; (омега – область допустимых значений) - Модель должна использовать только ту информацию, которая доступна;
- Модель должна быть достаточно простой, чтобы ее использование было возможно и целесообразно при исследовании операций.
Типы моделей:
- Описательная модель
- сценарии;
- таблицы;
- анкеты.
- Графические модели
- блок-схемы;
- графы состояний;
- сети;
- деревья.
- Физические модели
- аналоговые модели;
- масштабные модели.
- Математические модели
- аналитические;
- имитационные модели.
Этапы построение моделей:
- Определение множества переменных, которые существенно влияют на показатели эффективности операции;
- Выбор структуры, вида модели
Например,
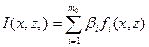 (функционал
(функционал  зависит от ряда функций)
зависит от ряда функций)
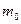 – обобщенный критерий.
– обобщенный критерий. - Оценка параметров коэффициентов
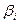 ;
; - Поиск решений.
Поиск решений
Задача заключается в поиске значений 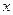 , который обеспечивает наибольшую эффективность операции в соответствии с целевой функцией
, который обеспечивает наибольшую эффективность операции в соответствии с целевой функцией  при выполнении ограничений
при выполнении ограничений
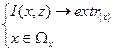 .
.
Варианты задачи поиска решений
- Известны значения переменных
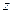 ,
,  , которые заданы следующим образом:
, которые заданы следующим образом:
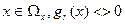 ;
; 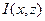 ,
, 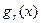 линейны по
линейны по 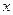 , тогда методами решения этой задачи являются методы линейного программирования;
, тогда методами решения этой задачи являются методы линейного программирования;- Если хотя бы одна из них не линейна по
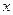 , то применяют методы нелинейного программирования;
, то применяют методы нелинейного программирования; - Если хотя бы одна из переменных
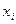 , где
, где 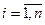 дискретна, то используют методы дискретного целочисленного программирования;
дискретна, то используют методы дискретного целочисленного программирования; - Если переменные
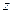 случайные величины и известны законы их распределения, то модель называется вероятностной и вместо детерминированной величины
случайные величины и известны законы их распределения, то модель называется вероятностной и вместо детерминированной величины 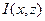 используют некоторые характеристики распределения случайной величины;
используют некоторые характеристики распределения случайной величины; - Если
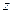 полностью неизвестная величина, то тогда методом поиска решения называются методы принятия решений в условиях неопределенности;
полностью неизвестная величина, то тогда методом поиска решения называются методы принятия решений в условиях неопределенности; - Если
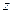 является результатом активного действия противника, то поиск решения осуществляется на основе математического аппарата теории игр.
является результатом активного действия противника, то поиск решения осуществляется на основе математического аппарата теории игр.
Корректировка модели
- Анализ модели с точки зрения разумности и приемлемости полученных решений;
- Анализ чувствительности моделей к малым вариациям исходных данных. (малые изменения исходных данных не должны резко менять решение).
Пример (продавец газет)
Пусть
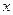 – число газет, взятых продавцом;
– число газет, взятых продавцом;
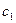 – прибыль за проданную газету;
– прибыль за проданную газету;
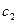 – убытки за непроданную газету;
– убытки за непроданную газету;
 – спрос на газеты;
– спрос на газеты;
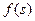 – плотность распределения спроса;
– плотность распределения спроса;
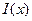 с – средняя прибыль, показатель эффективности продажи газет.
с – средняя прибыль, показатель эффективности продажи газет.
Составить математическую модель.
Дано:
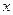 ,
, 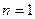 ; - количество продавцов
; - количество продавцов
 ,
, 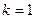 ; - спрос (неуправляемая переменная, случайная величина)
; - спрос (неуправляемая переменная, случайная величина)
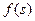 ;
;
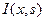 . - (мат. ожидание)
. - (мат. ожидание)
Решение:
Два случая:
1. все газеты продаются 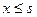 ;
;
2. газеты не продаются 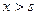 .
.
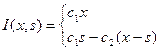 ;
;
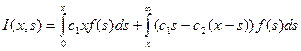 .
.
 2014-02-02
2014-02-02 436
436








