2014-02-02
521
Пример с условием 6
Пример с условием 5
Пример с условием 4
Пример с условием 3
Пример с условием 2
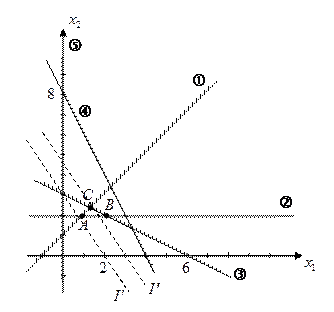
Решение:
.
.
; 
;
; 
.
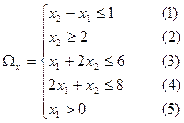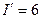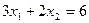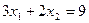Найдем координаты точки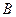 
:
;
;
;
;
.
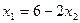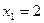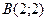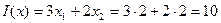Решение:
.
; ;
; .
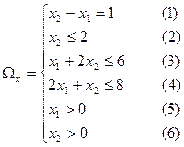
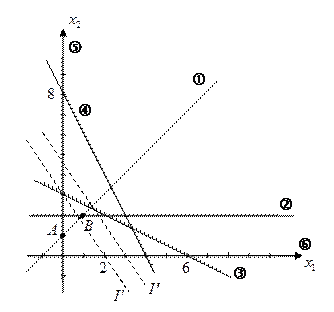
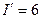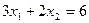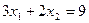Найдем координаты точки :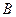
;
;
;
;
.
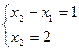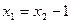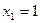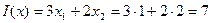Решение:
.
.
; ;
; .
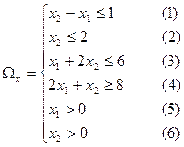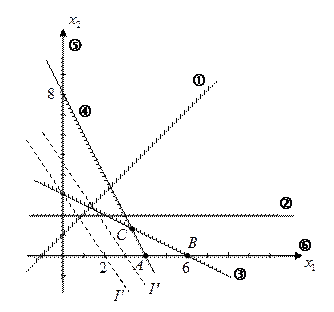
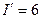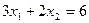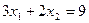Найдем координаты точки :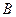
;
;
;
;
.
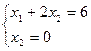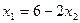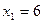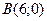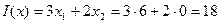Решение:
.
.
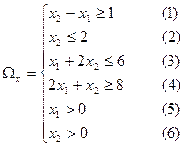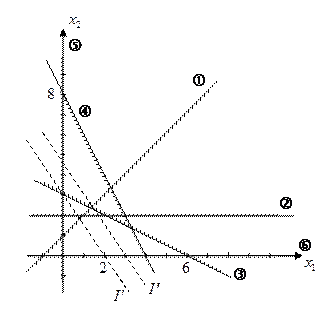
Нет допустимых решений.
Решение:
.
.
; 
;
; 
.
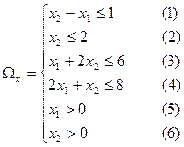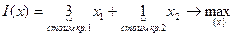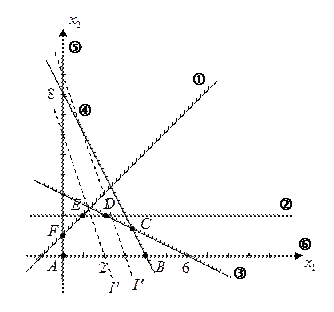
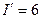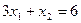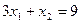Найдем координаты точки :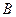
;
;
;
;
.
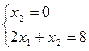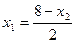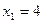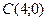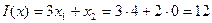Решение:
.
.
; 
;
; 
.
.
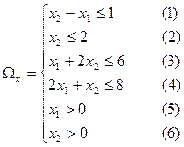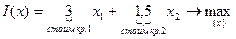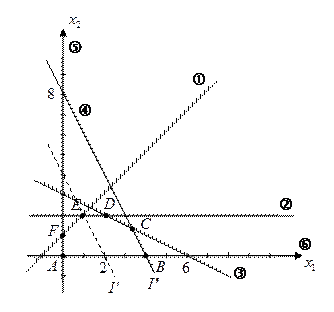
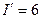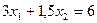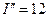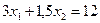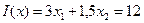Алгебраический метод решения задач линейного программирования (симплекс метод)
Возьмем систему из последнего домашнего задания
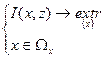
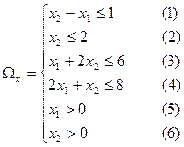
Общий метод решения задач ЛП называется Simplex(S)-метод. Информацию которую можно получить, не ограничивается оптимальными значениями переменно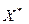й 
и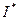 
т.к. он позволяет дать экономическую интерпретацию полученного решения и провести анализ модели на чувственность. S-метод носит итерационный характер: однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор пока не будет получено оптимальное решение. Для использования S-метода, мат. модель должна быть представлена в форме, которую называют линейной формой:
|
|
|
- все ограничения должны быть записаны в виде равенств с неотрицательной правой частью
- значения всех переменных должны быть неотрицательны
- целевая функция подлежит максимилизации и минимализации
Как привести математическую модель к стандартной форме:
- Для ограничения: меньше/равно
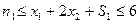
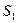- остаточная переменная
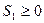- превращает ограничения типа неравенство в равенство и ее можно интерпретировать как остаток или неиспользованную часть ресурса
- Если ограничения: больше/равно, то для приведения к стандартному виду вычитается перемена, которая называется избыточная
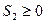//из левой части вычитаем
Преобразования целевой функции
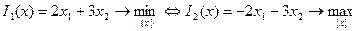
Пример:
Представить в стандартной форме
; 
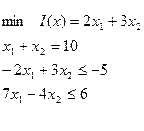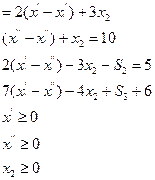
где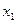 
- не имеет ограничений в знаке
При анализе графического метода решения задач ЛП было отмечено, что оптимальному решению всегда соответствует одна из угловых (экстремальных) точек пространства решения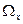 
. Именно этот результат и положен в основу S-метода. В S-методе реализуется упорядоченный процесс при котором, начиная с некоторой исходной (опорной), до,,,,, угловой точки, осуществляется последовательные переходы от одной экстремальной точки до другой, до тех пор, пока не будет найдена точка оптимального решения, Выбор каждой следующей точки определяется двумя параметрами:
- каждая последующая угловая точка должна быть смежна с предыдущей
- обратный переход к предшествующей экстремальной точки не может производиться
|
|
|
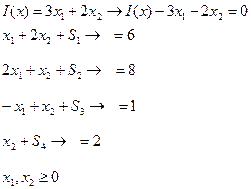
| свободные | базисные | |
| A |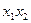 
| 
|
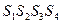
| B |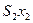 
| 
|
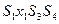
| C | 
| 
|
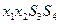
| D | 
| 
|
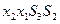
| E |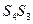 
| 
|
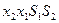
| F |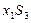 
| 
|
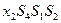
Две закономерности:
- Стандартная модель содержит 4 уравнения и 6 неизвестных,а т.к. число уравнений должно быть равно числу неизвестных, то в каждой экстремальной точке 2-е переменные должны иметь нулевые значения
- Смежные экстремальные точки отличаются только одной переменной в каждой группе (группы свободных базисных переменных)
Эти закономерности позволяют алгебраическим способом, путем преравнивания к нулю m-n переменных найти значения базисных переменных.
- если базисное решение удовлетворяет требованию неотрицательных правых частей, то оно называется допустимым базисным решением
Т.к. смежные точки отличаются только одной переменной- можно определить каждую последующую смежную экстремальную точку путем замены одной из текущих свободных переменных в базисные переменные (…)
