Тема: Общие направления развития ТАУ. 9 страница

Из приведенного доказательства вытекает следующие свойства:

· так как выходной сигнал у линейной части (ОУ) синусоидальный, то и во входном сигнале u нет смысла учитывать высшие гармоники, а достаточно только учета основной гармоники и сигнал u можно считать синусоидальным;

· так как при входном синусоидальном сигнале e нелинейности в выходном сигнале u достаточно учитывать лишь основную синусоидальную составляющую с частотой изменения входного сигнала, то нелинейный элемент обладает свойством линейного элемента, а именно, при входном синусоидальном сигнале выходной сигнал также синусоидальный. Следовательно, нелинейный элемент можно считать линейным и он должен иметь и передаточную функцию W_НЭ(p), и частотную характеристику W_НЭ(jw).

Еще раз отметим, что все эти свойства справедливы для автоколебательного режима и с учетом смысла приведенного доказательства.

Пусть W_ОУ(jw) - частотная характеристика объекта управления. Тогда в замкнутой САУ, приведенной на рис.36.1, в соответствии с критерием устойчивости Найквиста будут существовать незатухающие гармонические колебания (а в данном случае - автоколебания), если годограф частотной характеристики W_НЭ(jw)W_ОУ(jw) разомкнутой САУ пройдет (см. рис.7.4) через точку с координатами (-1, j0), что эквивалентно тому, что

W_НЭ(jw)W_ОУ(jw)=-1 (36.1)

Расчеты показывают, что выражении частотной характеристики W_НЭ(jw) нелинейности, получаемой путем замены р на jw в выражении передаточной функции W_НЭ(р), частота сократится и останется только амплитуда А входного синусоидального сигнала e. Поэтому частотная характеристика нелинейности называется амплитудной характеристикой W_НЭ(А) (это не одно и то же, что амплитудно-частотная характеристика линейного звена!), и условие (36.1) существования незатухающих гармонических колебаний перепишется в виде

W_НЭ(А)W_ОУ(jw)=-1 (36.2)

Выражение амплитудной характеристики имеет следующую структуру

W_НЭ(А)=q(А)+jq'(А), (36.3)

где q(А) и q'(А) - коэффициенты гармонической линеаризации, выражения которых для типовых нелинейностей приводятся в справочниках по ТАУ [8].

Выражение (36.2) содержит две неизвестные переменные амплитуду А и частоту w автоколебаний и, поэтому, является уравнением. Уравнение (36.2) в общем случае целесообразно решать графически, предварительно преобразовав его к виду

V_НЭ(A)=W_ОУ(jw), (36.4)

где V_НЭ(A)=-1/W_НЭ(A) - отрицательная обратная амплитудная характеристика нелинейности.

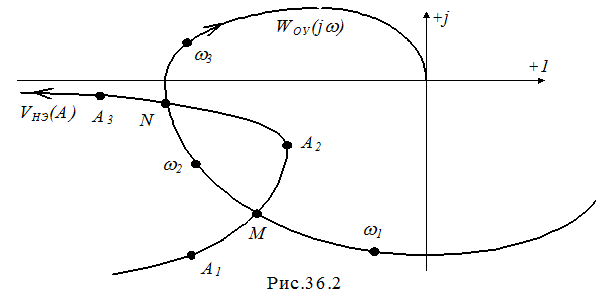
Для графического решения уравнения (36.4) на комплексной плоскости строятся годографы V_НЭ(A) и W_ОУ(jw). Необходимым условием существования автоколебаний является пересечение этих годографов (рис.36.2), например, в точках M и N. Однако не каждая точка пересечения соответствует устойчивым колебаниям. Достаточное условие существования автоколебаний формулируется следующим образом: если после точки пересечения годографов V_НЭ(A) и W_ОУ(jw) годограф V_НЭ(A) выходит из-под охвата годографом W_ОУ(jw), то решение в указанной точке устойчиво и ему отвечает автоколебания в нелинейной САУ. По этому условию на рис.36.2 автоколебания устойчивы с параметрами, определяемыми точкой N.

Частота автоколебаний w_N определяется из W_ОУ(jw) следующим образом. Годограф W_ОУ(jw) строится при изменении частоты, которая принимает, например, значения w₁, w₂, w₃ и т.д. Частота автоколебаний w_N находится, как следует из рисунка, между частотами w₂ и w₃. Для определения w_N проводятся дополнительно с малым шагом вычисления W_ОУ(jw) в интервале частот w₂... w₃ до тех пор, пока будет достигнуто достаточное по точности совпадение с точкой N.

Амплитуда автоколебаний A_N определяется таким же способом, как и частота w_N, но используется годограф V_НЭ(A) и амплитуды А₂ и А₃.

Если годографы V_НЭ(A) и W_ОУ(jw) не пересекаются, то автоколебаний нет. Если годографы V_НЭ(A) и W_ОУ(jw) касаются или сливаются на некотором участке, то вопрос о существовании автоколебаний остается открытым: автоколебания могут как быть, так и не быть. Для этого нужно провести дополнительное исследование нелинейной САУ другими методами.

Достоинство графического метода определения автоколебаний в том, что независимо от сложности передаточной функции объекта W_ОУ(р) и формы графика нелинейного элемента возможно определение амплитуды и частоты автоколебаний. В некоторых случаях уравнение (36.2) можно решить аналитически.

ИМПУЛЬСНЫЕ САУ

37. Достоинства импульсных САУ. Виды модуляции.

Виды импульсных элементов

Импульсными САУ называются такие, в которых носителем информации является импульс. Техническая реализация импульсных САУ сложнее реализации линейных нелинейных САУ при одинаковой элементной базе, но очень проста на основе микропроцессоров. В частности, импульсные САУ на основе механических элементов чрезвычайно редки и их возможности минимальные.

Импульсные САУ имеют следующие положительные качества:

· высокая точность и стабильность, обусловленная тем, что введенная в микропроцессор (именно о таком исполнении импульсной САУ реально можно говорить) информация обрабатывается без ошибок;

· высокая помехозащищенность информации, практическая нечувствительность к колебаниям температуры окружающей среды, колебаниям напряжения питания и другим возмущающим факторам;

· многоканальность, выражающаяся в том, что один микропроцессор может одновременно управлять множеством объектов в режиме разделения времени;

· дешевизна импульсных САУ на основе микропроцессоров.

Импульсные САУ работают в режиме периодического ввода и вывода информации. Если объектов управления несколько, то их обслуживание проводится по очереди: сначала вводится информация с 1-го объекта, обрабатывается и выводится на этот же объект, затем вводится информация с 2-го объекта, обрабатывается и выводится на этот же объект и так далее по всем объектам. Так как время обслуживания одного объекта намного меньше интервала (периода) между соседними подключениями к нему, то за время указанного периода микропроцессор успевает обслужить множество объектов (это называется режимом разделения во времени). Из-за высокой скорости работы микропроцессора (тактовая частота - десятки-сотни мегагерц), создается иллюзия того, что будто бы микропроцессор одновременно работает с несколькими устройствами сразу. На самом деле в каждый момент времени работа ведется только с одним объектом.

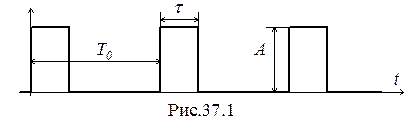
В импульсных САУ могут использоваться импульсы любой формы: прямоугольной, треугольной, трапециидальной, синусоидальной, экспоненциальной. Как носители информации все перечисленные и любые другие импульсы равноценны. Если учитывать простоту расчетов импульсных САУ и преимущественная их реализация на основе микропроцессоров, то наилучшими являются импульсы прямоугольной формы (рис.37.1). Последовательность прямоугольных импульсов характеризуется тремя параметрами: периодом следования Т₀, амплитудой А и длительностью t. Дополнительными параметрами являются относительная длительность g=t/T₀ и скважность Q=T₀/t импульсов.

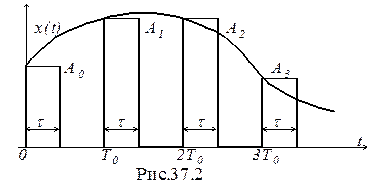
Импульсные САУ применяются для управления непрерывными объектами, в которых информация представлена в непрерывной, аналоговой форме. Процесс преобразования аналогового сигнала в импульсы, называется модуляцией. В соответствии с тремя характеристиками прямоугольных импульсов, с этими импульсами реализуется три вида модуляции АИМ, ШИМ и ЧИМ.

При амплитудно-импульсной модуляции (АИМ) значение аналогового сигнала x(t) преобразуется в величину амплитуды импульса А₀, А₁, А₂, А₃ и т.д., а период Т₀ и длительность t импульса постоянны (рис.37.2). С таким видом модуляции работают микропроцессорные импульсные САУ, в которых t=T₀. Расчеты САУ с этим видом модуляции самые простые.

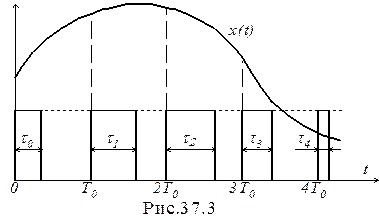
При широтно-импульсной модуляции (ШИМ) значение аналогового сигнала x(t) преобразуется в длительность импульса t₀, t₁, t ₂, t ₃ и т.д., а период Т₀ и амплитуда А импульса постоянны (рис.37.3). Такой вид модуляции применяется в таких импульсных САУ, в которых импульсы используются не только как носители информации с их обработкой в устройстве управления, но и поступают на силовые элементы, например на электродвигатели. В период действия импульса двигатель вращается, а при отсутствии - двигатель неподвижен.

При частотно-импульсной модуляции (ЧИМ) значение аналогового сигнала x(t) преобразуется в период следования импульсов Т₀, Т₁, Т₂, Т₃ и т.д., т.е. изменяется частота следования импульсов, а длительность t и амплитуда А импульса постоянны (рис.37.4). Такой вид модуляции самый помехоустойчивый и применяется в тех случаях, когда между управляющим устройством и объектом, датчиками, органами управления большие расстояния и из-за длинных линий связи в них высок уровень помех.

Модуляция аналогового сигнала осуществляется в импульсных элементах, называемых модуляторами. Вариантов исполнения модуляторов существует множество. Ниже рассмотрим две схемы амплитудных модуляторов.

До микропроцессоров амплитудные модуляторы выполнялись по схеме, приведенной на рис.37.5. Модулятор содержит запоминающий конденсатор С, ключ К и согласующий усилитель У. Управляется модулятор синхроимпульсами

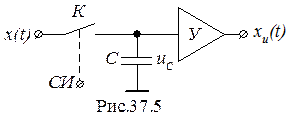
СИ, поступающими с периодом Т₀. По сигналу СИ кратковременно замыкается ключ К и конденсатор С заряжается до напряжения u_C, равного значению входного сигнала x(t) при t=nT₀, где n - номер импульса. После размыкания ключа конденсатор оказывается подключенным ко входу согласующего усилителя У. Согласующий усилитель имеет очень большое входное сопротивление порядка 10⁶...10⁷ Ом, очень малое выходное порядка 0,01...0,1 Ом и коэффициент усиления равный единице. Из-за большого входного сопротивления конденсатор С до прихода следующего синхроимпульса практически не разряжается, т.е. в течение времени Т₀ напряжение u_C=const. Также постоянным будет сигнал х_И(t). Сигнал х_И(t) будет иметь ступенчатую форму, которая получается из рис.37.2 при t=T₀.

Схема модулятора на основе микропроцессора приведена на рис.37.7.

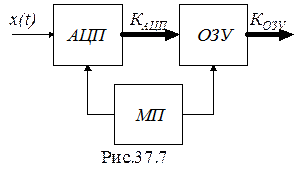
Аналоговый сигнал x(t) поступает на аналогово-цифровой преобразователь АЦП, в котором практически непрерывно аналоговый сигнал преобразуется в цифровой двоичный код К_АЦП, значение которого прямо пропорционально сигналу x(t). Цифровой код представляет собой совокупность сигналов вида 0 или 1 шины данных, состоящей из нескольких проводников, обычно 8...12 проводников. На рисунке шина выделена утолщением. По сигналам микропроцессора МП, следующих с периодом Т₀, сначала приостанавливается работа АЦП, а затем осуществляется запись кода К_АЦП в оперативное запоминающее устройство ОЗУ. Затем сигналы микропроцессора снимаются и АЦП возобновляет свою работу, а в ОЗУ сохраняется неизменным в течение времени Т₀ код К_ОЗУ. В этом модуляторе импульсы представлены в виде последовательности кодов К_ОЗУ. Импульсный сигнал ступенчатый, так как код сохраняется в течение времени Т_{0 .}

37. Импульсные регуляторы САУ

В импульсных САУ в модулированных импульсах заключена информация о значениях аналогового сигнала, которые он принимает в моменты времени кратные периоду Т₀. Информация о значениях аналогового сигнала, которые он принимает в промежутках времени между моментами съёма импульса, никак не учитывается и попросту теряется. В импульсных САУ это является погрешностью дискретизации, и уменьшить погрешность, очевидно, можно путем уменьшения периода Т₀ следования импульсов. Однако бесконечно уменьшать Т₀ не представляется возможным, так как в промежутке между соседними съемами импульсов нужно время на обработку введенной в управляющее устройство информации. Требования многоканальности ведет к еще большему увеличению Т₀.

Величина погрешности дискретизации определяется соотношением максимальной скорости изменения аналогового сигнала и периода Т₀. Самыми быстро протекающими процессами в судовых автоматических системах являются процессы в судовой электростанции. Как показывает практика даже здесь оправдано применение микропроцессора, как базового элемента импульсных САУ. Во всех остальных судовых установках автоматизации процессы протекают намного медленнее и применение микропроцессоров всегда эффективно.

В импульсных САУ в принципе можно реализовать все функции обработки информации, которые существуют в линейных, нелинейных и других типах САУ, но с отмеченными выше погрешностями дискретизации.

В САУ не импульсного типа основной формой описания элементов являются дифференциальные уравнения и в немногих случаях, а именно, для безинерционных звеньев - алгебраические уравнения. В импульсных САУ алгебраические уравнения остаются такими же, как и в не импульсных. Дифференциальные уравнения заменяются на разностные, которые получаются из обыкновенных дифференциальных уравнений путем замены в них производных следующими выражениями

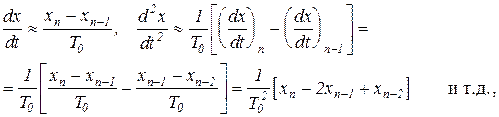(38.1)

где n - индекс последнего (текущего) импульса;

(n-1) - индекс предпоследнего импульса и т.д.

В выражениях (38.1) операции взятия производной сведены к четырем арифметическим действиям - сложения, вычитания, умножения и деления. Только эти математические действия реализуются командами микропроцессора и, поэтому, могут быть запрограммированы.

Особенности применения микропроцессоров МП в импульсных САУ рассмотрим на примере реализации импульсного регулятора по схеме, содержащей последовательно включенные микропроцессор и электродвигатель ЭД (рис.38.1) постоянного тока (ДПТ).

Выходным сигналом ЭД является угол a поворота его выходного вала. ЭД в этом случае является интегрирующим звеном с передаточной функций (19.7). С помощью программы, исполняемой микропроцессором, указанный регулятор может иметь необходимые динамические свойства, которые определяются видом передаточной функции регулятора.

Определим алгоритм программы МП так, что регулятор в целом представлял бы собой пропорционально-интегральный (ПИ-) регулятор с передаточной функцией

(38.2)

где k_P - коэффициент передачи пропорциональной (П-) части регулятор;

Т_И - постоянная времени интегральной (И-) части регулятора.

ПИ-регулятор является самым распространенным типом регулятора во всех САУ. Его достоинства в том, что за счет И-части обеспечивается нулевая статическая ошибка регулирования в замкнутых САУ, а применение П-части обеспечивает запас устойчивости САУ и стабильные эксплуатационные характеристики.

Так как МП и ЭД включены последовательно, то

W_P(p)=W_МП(р)W_ЭД(р) (38.3)

Из (38.3) с учетом (38.2) и (19.7) рассчитываем передаточную функцию микропроцессора

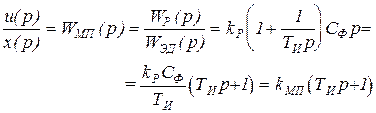(38.4)

Из (38.4) следует операторное и дифференциальное уравнения вида

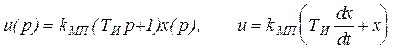(38.5)

Выполняем замену производной согласно (38.1) и получаем разностное уравнение

(38.6)

Это разностное уравнение описывает работу микропроцессора, с помощью которого значение u_n текущего импульса на выходе микропроцессора определяется через текущее x_n и предпоследнее x_n-1 значения входного сигнала.

Алгоритм вычислений по этому разностному уравнению приведен на рис.38.2.

При выполнении программы на вход электродвигателя ЭД поступает последовательность импульсов напряжения величиной u₀, u₁,... u_n (рис.38.3, график а).

Если в качестве ЭД применен двигатель постоянного тока (ДПТ), то в течение времени Т₀ его вал повернется на угол a_n, пропорциональный напряжению u_n (рис.38.3, график б). Вид модуляции сигнала u амплитудно-импульсный (АИМ).

Если в качестве ЭД использовать асинхронный двигатель (АД), который намного надежнее и дешевле ДПТ, то частоту вращения и, следовательно, скорость изменения угла поворота его вала уже невозможно будет регулировать через изменение величины подводимого к двигателю напряжения u. Для реализации с АД такого же изменения угла a как и с ДПТ, нужно сменить вид модуляции выходного сигнала МП - перейти от АИМ к ШИМ (рис.38.3, график в). АД в течение времени действия импульса напряжения u поворачивается на тот же угол (рис.38.3, график г), что и при использовании ДПТ. Чем больше угол поворота АД, тем больше длительность t_n приложения к двигателю постоянного напряжения u_АД.

Длительность t_n импульса связана с вычисленным по (38.6) значением напряжения u_n соотношением

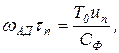(38.7)

где w_АД - номинальная частота вращения АД.

Соотношение (38.7) можно доказать, рассмотрев любой интервал длительностью Т₀, например, интервал времени от 2Т₀ до 3Т₀ (рис.38.3). Угол поворота a₁₂ для ДПТ равен T₀u₂/C_ф Угол поворота a₁₃ для АД равен w_АДt₂. Так как a₁₂ = a₁₃, то из этого равенства следует (38.7).

Подставив в (38.7) выражение u_n из (38.6) и решив полученное уравнение относительно t_n, получим длительность включения АД в момент действия n -го импульса

(38.8)

Согласно последнего выражения микропроцессор вводит очередное значение x_n входного сигнала x, извлекает из памяти предшествующее значение x_n-1 входного сигнала, вычисляет значение t_n и включает в течение этого времени в работу асинхронный двигатель. Алгоритм вычисления t_n подобен тому, который приведен на рис.38.2.

ОПТИМАЛЬНЫЕ И АДАПТИВНЫЕ САУ

39. Основные понятия оптимальных САУ

Под оптимальной понимается такая САУ, которая является наилучшей по совокупности нескольких показателей качества с учетом ограничений на внутренние сигналы и сигналы управления. В практике применения САУ используются различные частные показатели качества, такие как ошибки регулирования e_ст, e_ск, длительности процессов t_Р, t_ПП, t_Н, перерегулирование s, экономичность, производительность, надежность и др. Смысл обобщенного показателя качества по совокупности частных показателей заключается в том, ни по одному из частных показателей не достигается экстремум, а по совокупности экстремум достигается. Такой экстремум достигается за счет компромисса между частными показателями качества, когда степени приближения их к своим экстремальным значениям примерно одинаковы у всех показателей с учетом их значимости. Выбор частных и обобщенного показателя качества производится человеком исходя из его практических потребностей. В общем случае никакие методы ТАУ не позволяют сформулировать требования к качеству САУ.

Задачи, решаемые в теории оптимальных САУ, - это всегда задачи синтеза. Общая формулировка задачи следующая:

К системе, описываемой системой дифференциальных уравнений

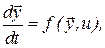(39.1)

где - множество внутренних сигналов системы, приложен управляющий сигнал u. На внутренние сигналы y_i и управления u могут быть наложены ограничения типа >, <, ³, £ и интегральные ограничения.

Необходимо систему за интервал времени t₀...t₁ перевести из начального состояния 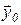в конечное 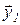так, чтобы достигался бы минимум функционала вида

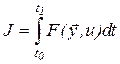(39.2)

Функционал в данном случае является обобщенным показателем качества.

В решения сформулированной задачи определяется оптимальная траектория, переводящая систему из 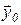в 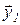, и соответствующий этой траектории оптимальный закон изменения сигнала управления u без предварительного задания структуры управляющего устройства. Во всех ранее рассмотренных САУ ситуация прямо противоположная, а именно, сначала задается структура управляющего устройства и закон изменения формируемого им сигнала u, а затем вычисляются траектории, на которых производится оценка показателей качества, и, изменяя характеристики нескольких звеньев, добиваются наилучших показателей.

Поясним эти особенности на примере. Пусть в некоторой САУ при применении заданного типа регулятора достигнуто заданное время t_ПП переходного процесса на траектории 1 перехода из начальной у₀ в конечную у₁ точку (рис.39.1а). Если изменить настройки регулятора, то в принципе можно за то же время t_ПП снова перейти из начальной точки у₀ в конечную у_{1 ,} но уже по другой траектории 2. Можно применить другой тип регулятора с тем же результатом, но с траекторией 3. Очевидно, что таких траекторий, переводящих систему за время t_ПП из начальной точки у₀ в конечную у_{1 ,} существует бесконечно много. Каждой

траектории соответствует свой закон изменения управляющего сигнала (рис.39.1б), причем число таких траекторий бесконечно. В смысле достижения конечного результата - перевода системы из начальной точки у₀ в конечную у₁ за за время t_ПП - все управления (рис.39.1б) и все траектории (рис.39.1а) равноценны. Однако при введении еще одного показателя качества, например, расходе энергии при движении по траектории из указанных траекторий можно выбрать наилучшую. Следовательно, каждой траектории в целом сопоставляется числовая характеристика. С помощью такой числовой характеристики можно сравнивать между собой отдельные траектории. В оптимальных САУ такой числовой характеристикой траектории является функционал J (39.2).

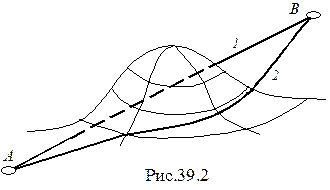Следующий пример (рис.39.2): необходимо из пункта А попасть в пункт В кратчайшим путем. Если А и В расположены на плоскости, то кратчайшим путем, очевидно, будет прямая линия 1. Если между А и В имеется возвышенность произвольной формы, то кратчайший путь 2 пройдет частично сбоку по склону возвышенности. Аналитическое определение формы пути 2 является типичной задачей теории оптимального управления.

После определения оптимального закона изменения управляющего сигнала u формируется структура управляющего устройства и определяются его параметры. Такой метод расчета управляющего устройства имеет то достоинство, что устройство создается под заведомо наилучший закон изменения сигнала u.

Указанную специфику задач оптимальных САУ проследим на примере.

Пусть имеется САУ любого типа, в которой сигнал ошибки e регулирования, определяемый как разность между заданным и действительным значениями регулируемого сигнала, может изменяться по любому закону (рис.39.3), причем установившееся значение e(¥)=0. Введем оценку качества графика e(t) следующим функционалом

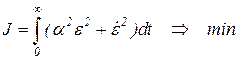(39.3)

Составляющая e² при минимизации J обеспечивает определение такого графика e, который с осью t образует фигуру с наименьшей площадью, причем площади как выше, так и ниже оси учитываются со знаком плюс. Минимум площади обеспечивает наискорейшее приближение графика к оси t, т.е. максимальное быстродействие (это 1-й частный показатель качества). Составляющая при минимизации J обеспечивает исключение из возможных графиков таких, у которых имеются высокочастотные колебания. Минимум по - это подавление высокочастотных сигналов внутри системы, что обеспечивает устойчивую работу дифференцирующих звеньев САУ и уменьшает механический износ элементов САУ (это 2-й частный показатель качества). Коэффициент a² - это весовой коэффициент, числовое значение которого учитывает значимость составляющей e² в функционале: если a²=0, то составляющая e² не принимается во внимание при определении оптимальной траектории; если a² очень велика, то в функционале главной является составляющая e².

Вид функции e(t), при которой достигается минимум функционала, находится из следующих преобразований:

(39.4)

В выражение J входит постоянная величина 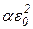, значение которой не зависит от вида траектории сигнала e, и интеграл от выражения 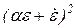, которое неотрицательно, т.е. либо ноль, либо положительное число. Указанный интеграл примет минимум, равный 0, на траектории, на которой везде