Введем понятие решетчатой функции времени 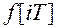 или в сокращенной записи
или в сокращенной записи 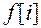 , значения которой определены в дискретные моменты времени
, значения которой определены в дискретные моменты времени 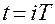 , где
, где 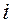 – целое число,
– целое число, 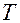 – период повторения.
– период повторения.
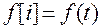 при
при 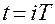 .
.
Если в относительных единицах, то 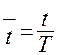 .
.
Ординаты решетчатой функции – это дискреты в моменты времени 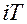 .
.
Дискреты 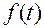 могут быть определены для смещенных моментов времени
могут быть определены для смещенных моментов времени 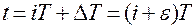 , где
, где 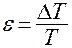 – относительное смещение.
– относительное смещение.
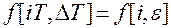
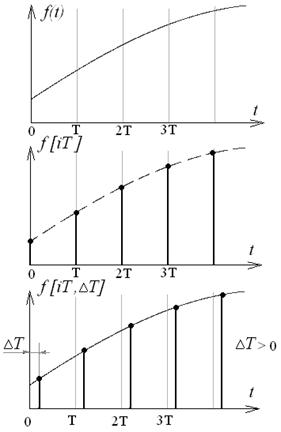
Рис. 1.22
Действия, производимые со смещенными решетчатыми функциями, выполняются по тем же правилам, что и для несмещенных. Поэтому далее будем рассматривать несмещенные решетчатые функции.
При 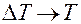 , решетчатая функция превращается в непрерывную.
, решетчатая функция превращается в непрерывную.
Любая числовая последовательность некоторой величины может быть представлена решетчатой функцией.
Обратная задача (формирование непрерывной функции из решетчатой) не может быть решена однозначно, так как функции, заданной в дискретные моменты времени, может соответствовать бесконечное множество непрерывных функций.
Непрерывные функции, совпадающие с заданными решетчатыми называются огибающими решетчатой функции.
Основная огибающая – непрерывная функция, совпадающая с заданными дискретами, которая может быть получена как результат решения дифференциального уравнения, порядок которого наименьший по сравнению с другими огибающими.
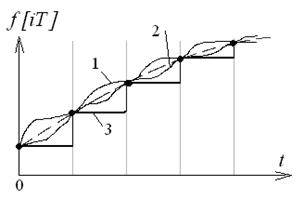
Рис. 1.21
Здесь 3 - ступенчатая функция соответствует экстраполятору нулевого порядка.
Пример. 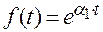 ,
, 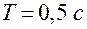 .
.
Записать выражение для 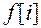 .
.
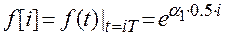
Пример. 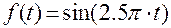 ,
, 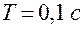 .
.
Записать выражение для 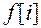 .
.
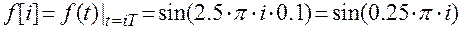 .
.
 2014-02-02
2014-02-02 702
702








