2014-02-02
596
Математическое описание амплитудно-импульсной системы
По аналогии с линейными непрерывными системами, процессы в которых описываются линейными дифференциальными уравнениями с постоянными коэффициентами для импульсных систем применимы разностные уравнения (или уравнения в конечных разностях).
В общем виде:
.
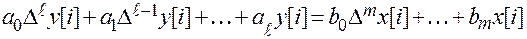Для реальных физически реализуемых систем порядок разности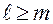 
.
Разности решетчатой функции могут быть выражены через значения самой решетчатой функции, аргументы которой сдвинуты вдоль оси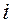 
на некоторое число тактов, в этом случае получают другую форму записи уравнений
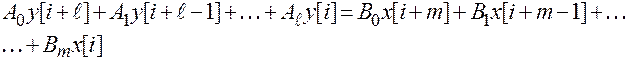Такую форму записи называют рекуррентным уравнением или разностным уравнением в рекуррентной форме. Порядок разностного уравнения определяется величиной 
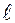выходной решетчатой функции в рекуррентном уравнении.
Рассмотрим пример.
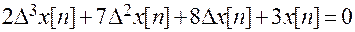
Перепишем это уравнение в рекуррентной форме.
.
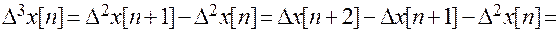
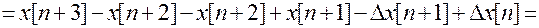
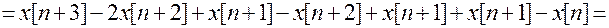
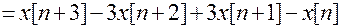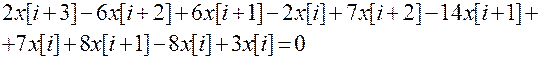
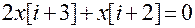
Таким образом, порядок уравнения определяется по рекуррентной форме и равен максимальному сдвигу.
