Операторная форма записи разностных уравнений.
Введем обозначения:
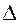 - оператор разности,
- оператор разности,
Z – оператор смещения решетчатой функции на один такт.
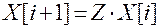 ,
,
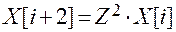 .
.
Связь операторов 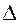 и Е.
и Е.
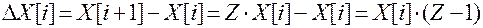 ,
,
отсюда 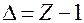 или
или 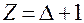 .
.
Пример. Преобразуем уравнение в рекуррентную форму.
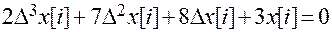
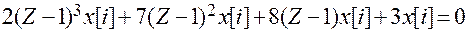
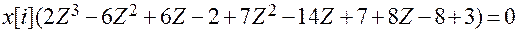
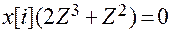 .
.
Отсюда 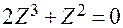 или
или 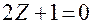
Тогда 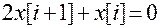 .
.
Так же как и в случае дифференциальных уравнений, решение разностного уравнения ищется в виде суммы двух составляющих:
1) общее решение однородного разностного уравнения;
2) частное решение неоднородного уравнения с правой частью.
Для разностного уравнения так же существует понятие характеристического уравнения.
Общее решение однородного уравнения имеет вид:
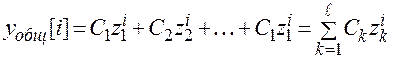 ,
,
где 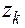 (k = 1,2,…,
(k = 1,2,…,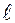 ) – корни характеристического уравнения.
) – корни характеристического уравнения.
Исходное уравнение:
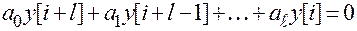
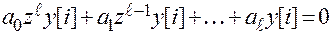
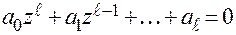 - характеристическое уравнение.
- характеристическое уравнение.
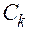 – произвольные постоянные, определяемые из начальных условий.
– произвольные постоянные, определяемые из начальных условий.
Частное решение неоднородного уравнения.
Если в правой части уравнения стоит константа, то решение ищется в виде постоянной.
Если в правой части уравнения полином относительно 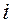 , то и решение ищется в виде полинома того же порядка.
, то и решение ищется в виде полинома того же порядка.
Пример.
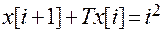
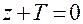 . Отсюда
. Отсюда 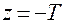 .
.
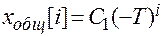
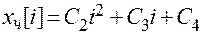
Подставим в исходное уравнение частное решение
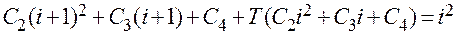
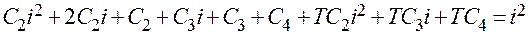
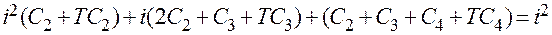
Отсюда 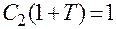 или
или 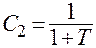 .
.
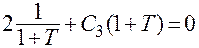 , тогда
, тогда 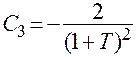 .
.
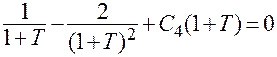 , тогда
, тогда 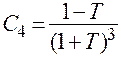 .
.
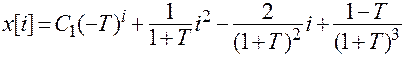
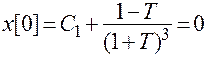 .
.
Отсюда 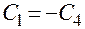 .
.
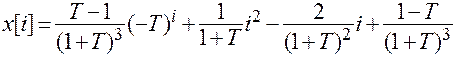 .
.
 2014-02-02
2014-02-02 2518
2518
