Над решетчатыми функциями применяются операции дифференцирования и интегрирования.
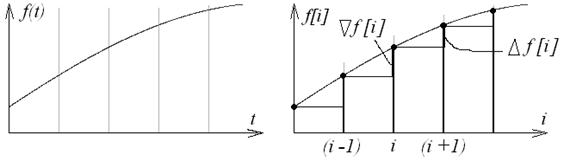
Рис. 1.22
Аналогом первой производной непрерывной функции для решетчатой функции является первая прямая разность: 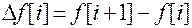 или обратная:
или обратная: 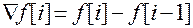 .
.
Аналог производной второго порядка – разность второго порядка (2-ая разность):
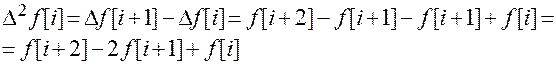 Для разности порядка К:
Для разности порядка К:
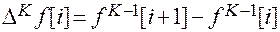 .
.
Аналогом интеграла непрерывной функции от 0 до t для решетчатой функции является сумма решетчатых функций:
 .
.
Операция суммирования - обратная операция по отношению к разности.
Определим разность для суммы
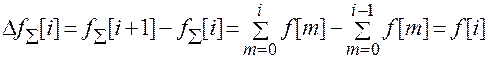
Пример. 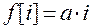 - решетчатая функция.
- решетчатая функция.
Найти сумму этой функции.
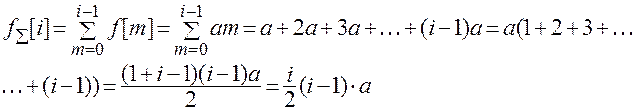
 2014-02-02
2014-02-02 938
938








