Z-преобразование. Математическое описание и анализ импульсной системы с амплитудной модуляцией существенно упрощаются, если все сигналы в системе (как в импульсной, так и в непрерывной части) рассматривать только в дискретные моменты времени t = 0 T; 1 T; 2 Т;...; I T;...; 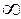 . При этом каждый непрерывный сигнал
. При этом каждый непрерывный сигнал 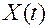 удобно представлять в виде решетчатой функции времени
удобно представлять в виде решетчатой функции времени 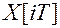 значения которой определены только для дискретных моментов времени:
значения которой определены только для дискретных моментов времени:
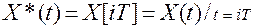
Между дискретными значениями аргумента t функция 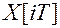 равна нулю.
равна нулю.
Непрерывная функция 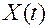 является огибающей для решетчатой функции
является огибающей для решетчатой функции 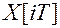 , и каждому конкретному сигналу
, и каждому конкретному сигналу 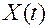 соответствует вполне определенный сигнал
соответствует вполне определенный сигнал 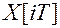 .
.
При замене реальных непрерывных сигналов решетчатыми функциями часто удобнее переходить к относительному времени  , т. е. измерять время числом периодов квантования Т. В этом случае относительный период
, т. е. измерять время числом периодов квантования Т. В этом случае относительный период 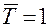 , а решетчатая функция обозначается
, а решетчатая функция обозначается 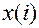 .
.
Последовательность неединичных импульсов, образующих решетчатую функцию на интервале 0 < iT < ¥, можно представить в виде бесконечного ряда
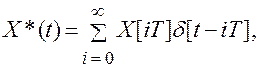 (2.1)
(2.1)
где 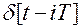 — смещенная дельта-функция, существующая только в моменты времени
— смещенная дельта-функция, существующая только в моменты времени 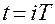 и равная нулю при всех других значениях t.
и равная нулю при всех других значениях t.
Применим к сумме (2.1) преобразование Лапласа, учитывая при этом, что изображение суммы оригиналов равно сумме их изображений, а также, что согласно теореме запаздывания изображение смещенной дельта-функции равно 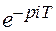 . Тогда изображение решетчатой функции (2.1) по Лапласу:
. Тогда изображение решетчатой функции (2.1) по Лапласу:
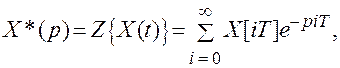 (2.2)
(2.2)
Выражение (2.2) называется дискретным преобразованием Лапласа. Оно содержит трансцендентный сомножитель 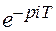 , из-за которого изображения
, из-за которого изображения 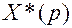 и соответствующие передаточные функции становятся иррациональными функциями аргумента р, что создает определенные трудности при их использовании. Поэтому с целью получения передаточных функций импульсных систем в дробно-рациональной форме, свойственной непрерывным системам, целесообразна замена аргументов
и соответствующие передаточные функции становятся иррациональными функциями аргумента р, что создает определенные трудности при их использовании. Поэтому с целью получения передаточных функций импульсных систем в дробно-рациональной форме, свойственной непрерывным системам, целесообразна замена аргументов 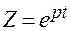 и тогда вместо (2.2) получают более удобное для практического использования преобразование, называемое z -преобразованием решетчатой функции (или дискретной последовательности)
и тогда вместо (2.2) получают более удобное для практического использования преобразование, называемое z -преобразованием решетчатой функции (или дискретной последовательности) 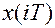 .
.
 (2.3)
(2.3)
Для большинства встречающихся в расчетах решетчатых функций z -преобразование может быть выполнено при помощи таблиц соответствия, которые приводятся в специальной литературе по импульсным системам. В табл. 2.1 приведены z -изображения лишь для функций времени, используемых далее в примерах.
Главное достоинство и удобство z -преобразования заключается в том, что сама запись z -изображения (2.3) указывает простой способ выполнения прямого и обратного преобразования:
1) чтобы по известной функции времени 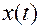 найти ее z -изображение, необходимо лишь каждое дискретное значение
найти ее z -изображение, необходимо лишь каждое дискретное значение 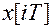 умножить на
умножить на 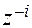 , а затем свернуть получившийся степенной ряд в конечную сумму;
, а затем свернуть получившийся степенной ряд в конечную сумму;
2) чтобы по известному изображению 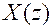 найти соответствующий сигнал
найти соответствующий сигнал 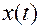 , необходимо представить изображение
, необходимо представить изображение 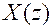 в виде степенного ряда по убывающим степеням
в виде степенного ряда по убывающим степеням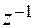 , получающиеся при этом числовые коэффициенты ряда и есть дискретные значения
, получающиеся при этом числовые коэффициенты ряда и есть дискретные значения 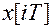 сигнала
сигнала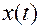 .
.
 2014-02-02
2014-02-02 983
983








