2014-02-02
632
Таблица 2.1 z-изображения простейших функций времени
| X(t) (t>=0) | X(iT) | X(p) | X(z) |
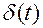1(t)
t
|
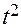
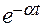
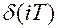
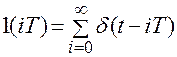iT
|
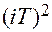
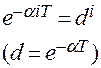
1/ p
|
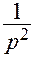
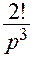
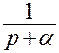
z / z -1
|
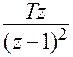
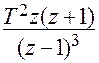
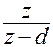
Обратное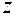 
-преобразование
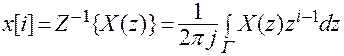
Интегрирование ведется по окружности радиуса r, внутри которой лежат все полюсы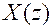 
.
Проиллюстрируем эти правила на простых функциях.
Пример. Найдем z -изображение единичной ступенчатой функции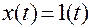 
. Соответствующая ей последовательность идеальных импульсов
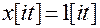, i = 0;1;2;3;…
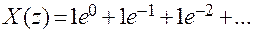(2.4)
Сумма бесконечного ряда (2.4) можно записать в компактной форме
,
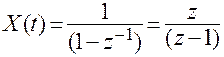что и приведено в таблице 2.1.
Пример. Найдем функцию времени 
, изображение которой
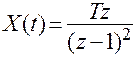(2. 5)
Делением числителя на знаменатель выражение (2.5) можно представить в виде ряда
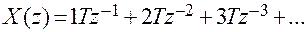
В соответствии с правилом 2 значение решетчатой функции
; 
; 
; …
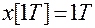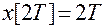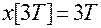или
.
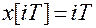Откуда нетрудно установить, что
.
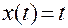Полученное соответствие также приведено в таблице 2.1.
