2014-02-02
614
Устойчивость импульсных систем
Динамические свойства импульсных систем с амплитудной модуляцией во многом аналогичны динамическим свойствам непрерывных систем. Поэтому методы анализа таких импульсных систем являются аналогами соответствующих методов исследования непрерывных систем.
Устойчивость импульсной системы управления, как и устойчивость непрерывной системы, определяется характером её свободного движения. Импульсная система устойчива, если свободная составляющая переходного процесса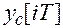 
с течением времени затухает, т.е. если
.
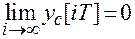Свободная составляющая 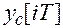является решением однородного разностного уравнения
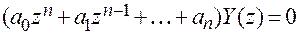. (3. 1)
Решением уравнения (3.1) при отсутствии у него одинаковых корней z представляет собой сумму:
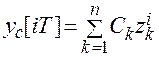, (3.2)
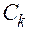– постоянные интегрирования, зависящие от начальных условий; 
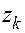– корни характеристического уравнения.
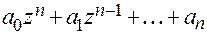= 0. (3.3)
Из выражения (3.2) видно, что при i →∞ решение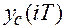 
стремится к нулю лишь в том случае, если все корни 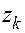по модулю меньше единицы, т.е. если
|
|
|
. (3.4)
Запись (3.4) выражает общее условие устойчивости: для устойчивости импульсной системы необходимо и достаточно, чтобы все корни характеристического уравнения системы находились внутри круга единичного радиуса с центром в начале координат
Если хотя бы один корень 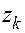располагается на окружности единичного радиуса, то система находится на границе устойчивости. При |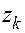|>1 система неустойчива.
Таким образом, единичная окружность в плоскости корней 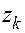является границей устойчивости и, следовательно, играет такую же роль, как мнимая ось в плоскости корней 
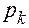(рис. 3.1, б). Этот вывод вытекает также из основной подстановки метода z -преобразования. Действительно, пусть 
. Тогда
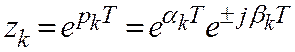
и требование |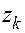|<1 сводится к неравенству:
, (3.5)
откуда следует известное в теории непрерывных систем условие устойчивости: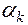 
<0.
Для суждения об устойчивости импульсных систем можно использовать обычные критерии устойчивости линейных систем, но при этом приходится учитывать лишь некоторые особенности импульсных систем. Так, для того чтобы применить критерий Гурвица, необходимо предварительно в уравнении (3.3) произвести замену переменной z на переменную w путем подстановки
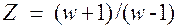(3.6)
И получить преобразованное характеристическое уравнение
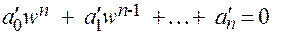(3.7)
Корням уравнения (3.3), расположенным в плоскости корней внутри единичного круга (см. рис. 3.1, а), теперь будут соответствовать корни преобразованного уравнения (3.7), находящиеся в плоскости корней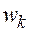 
слева от мнимой оси. Действительно, если |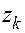|<1, то модуль числителя в выражении (3.6) должен быть меньше модуля знаменателя, т.е.
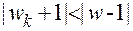. А это возможно лишь в том случае, если вектор 
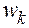расположен в левой полуплоскости (см. рис. 3.1, в).
|
|
|
