Частотный критерий устойчивости Михайлова. При использовании критерия Михайлова в характеристический полином подставляют , изменяют w от 0 до π/T и в комплексной плоскости строят годограф вектора

При использовании критерия Михайлова в характеристический полином 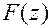подставляют 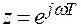, изменяют w от 0 до π/ T и в комплексной плоскости строят годограф вектора F (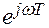). Импульсная система устойчива, если при возрастании w от 0 до π/T характеристический вектор F (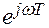) повернется против часовой стрелки на угол n π. Если годограф характеристического вектора проходит через начало координат, то система находится на границе устойчивости.

Рис. 3.1 Области устойчивости в плоскости корней.

Годографы вектора F (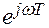) для устойчивой и неустойчивой системы второго порядка показаны на рис. 3.2, а.

Имеем характеристический полином:

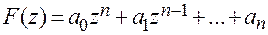
Подставим 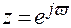при Т =1 и учитывая, что 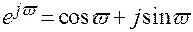, в результате получим ,

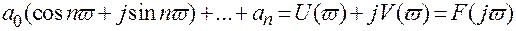Изменяя частоту v от 0 до p получим кривую – годограф вектора Михайлова.

Необходимое условие устойчивости:

Характеристический полином

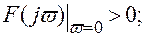
при четном n

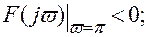при нечетном n

Отметим, что импульсные системы второго и даже первого порядка, в отличие от непрерывных систем такого же порядка, могут быть неустойчивыми при положительных коэффициентах характеристического уравнения. Это объясняется тем, что фиксатор, содержащийся обычно в контуре импульсной системы, вносит дополнительное отставание по фазе.