Пусть линейное разностное уравнение имеет вид:
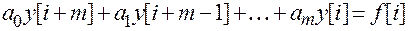 .
.
Для решения должны быть заданы значения 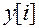 в первые моменты времени (m-1)
в первые моменты времени (m-1)
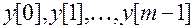 .
.
Перепишем исходное уравнение относительно z -изображений 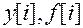
 ,
,
где 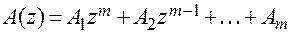 - характеристическое уравнение,
- характеристическое уравнение,
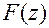 - изображение входного сигнала,
- изображение входного сигнала,
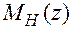 - обусловлен начальными условиями.
- обусловлен начальными условиями.
В общем случае 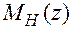 - полином порядка n, коэффициенты которого зависят от начальных условий. При нулевых начальных условиях
- полином порядка n, коэффициенты которого зависят от начальных условий. При нулевых начальных условиях 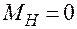
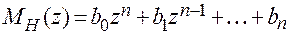
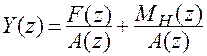 ,
,
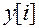 - определим в результате обратного z -преобразования
- определим в результате обратного z -преобразования
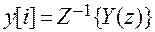
1) Для определения 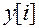 можно разложить
можно разложить 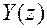 на простые дроби и воспользоваться таблицами.
на простые дроби и воспользоваться таблицами.
2) Если нас не интересует аналитическое выражение 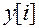 , а только конкретные значения
, а только конкретные значения 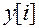 при
при 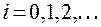 , то можно разложить
, то можно разложить 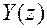 в ряд Лорана по убывающим степеням z.
в ряд Лорана по убывающим степеням z.
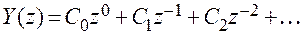 .
.
Это следует из определения z -преобразований
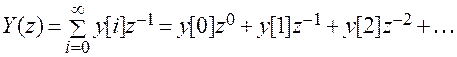 .
.
Пример. 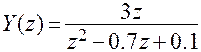 ;
; 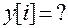
Представим в виде суммы двух дробей

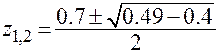 ,
, 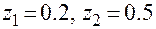 .
.
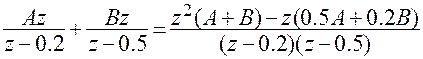
Отсюда 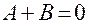 ,
, 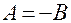 ;
; 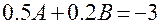 .
.
Тогда 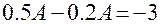 .
.
Значит 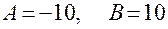 .
.
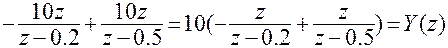
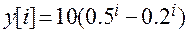 .
.
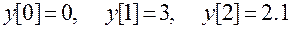 .
.
Пример. Разложим в ряд Лорана.
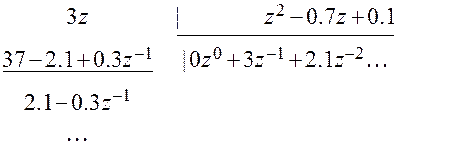
Отсюда 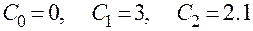 .
.
 2014-02-02
2014-02-02 1056
1056








