Для определения д.п.ф. замкнутой импульсной системы можно использовать правила структурных преобразований типовых соединений, сформулированные для непрерывных систем. Но при этом следует помнить, что:
1) обычные правила структурных преобразований справедливы для импульсных систем, лишь если каждая ветвь типового соединения представляет собой типовую импульсную цепь, состоящую из идеального квантователя (на входе цепи) и непрерывной части;
2) при иной структуре цепи и всего типового соединения эквивалентная д.п.ф. определяется более сложными правилами. Для основной схемы одноконтурной импульсной системы д.п.ф. по каналу д - х.

Рис. 2.3
Пусть для системы с единичной обратной связью (рис. 2.3) определена (для общего случая 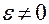 ) передаточная функция разомкнутой системы
) передаточная функция разомкнутой системы 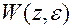 . Тогда изображение выходной величины
. Тогда изображение выходной величины
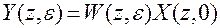 , (2.14)
, (2.14)
где 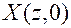 - изображение ошибки, так как ИЭ реагирует на значения Х в дискретные моменты времени
- изображение ошибки, так как ИЭ реагирует на значения Х в дискретные моменты времени 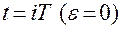 . При
. При 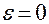 имеем
имеем 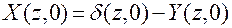 , подставляя его в (2.13), получим:
, подставляя его в (2.13), получим:
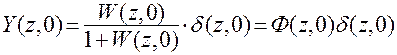 ,
,
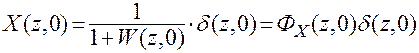 ,
,
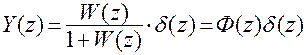 ,
,
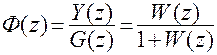 ; (2.15)
; (2.15)
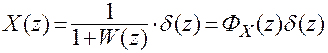 ,
,
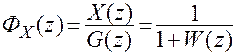 (2.16)
(2.16)
где 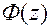 - передаточная функция замкнутой системы,
- передаточная функция замкнутой системы,
 - передаточная функция замкнутой системы по ошибке.
- передаточная функция замкнутой системы по ошибке.
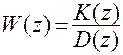 - д.п.ф. разомкнутого контура, представляющего собой (в данной схеме) типовую импульсную цепь.
- д.п.ф. разомкнутого контура, представляющего собой (в данной схеме) типовую импульсную цепь.
Характеристическое уравнение импульсной системы
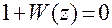
или в развернутых формах
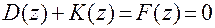
Характеристическое уравнение:
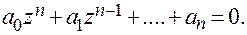
Условием применимости полученных формул является требование равенства 0 приведенной весовой функции в момент 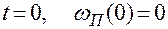 . Для этого в системах с бесконечно короткими импульсами в виде
. Для этого в системах с бесконечно короткими импульсами в виде 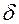 -функций требуется, чтобы степень числителя передаточной функции
-функций требуется, чтобы степень числителя передаточной функции 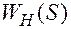 по крайней мере на два была меньше степени знаменателя.
по крайней мере на два была меньше степени знаменателя.
В системах с конечными по длительности импульсами достаточно чтобы разность была бы не меньше, чем 1.
Передаточные функции 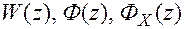 – могут быть использованы для оценки устойчивости и качества импульсных систем.
– могут быть использованы для оценки устойчивости и качества импульсных систем.
Если 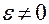 , то учитывая, что
, то учитывая, что 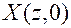 – изображение ошибки
– изображение ошибки
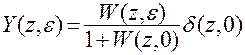 . Это выражение практически не используется.
. Это выражение практически не используется.
Кроме того, 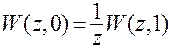 .
.
Для случая неединичной обратной связи, рис. 2.4.

Рис. 2.4
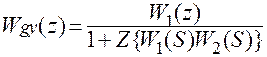 .
.
Пример. Определим характеристики замкнутой импульсной системы, разомкнутый контур которого соответствует цепи, содержащей «ключ», фиксатор и идеальный интегратор.
Подставляя точную д.п.ф. (2.13) в формулы (2.15) и (2.16), получим соответствующие д.п.ф. замкнутой системы:
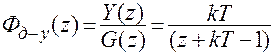 ; (2.17)
; (2.17)
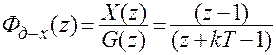 . (2.18)
. (2.18)
Характеристическое уравнение системы:
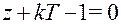 .
.
Найдем операторное уравнение динамики системы по каналу д-х. Разделив предварительно числитель и знаменатель д.п.ф. (2.18) на z, получим
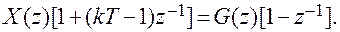 (2.19)
(2.19)
Уравнению (2.19) соответствует разностное уравнение в рекуррентной форме (при Т =1):
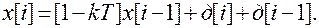
 2014-02-02
2014-02-02 643
643








